对三次曲线的研究最早始于艾萨克牛顿(Isaac Newton). 三次曲线的图像并不是一个椭圆. 称它们为椭圆曲线(elliptic curve), 是源自一类称为椭圆函数的积分, 这类积分的被积函数包含三次多项式的平方根.

对于椭圆曲线 $y^2=x^3+px+q$, 判别式 $\Delta=-16\bigl(4p^3+27q^2\bigr)$ 用于判别曲线的连通分支个数. 例如研究椭圆曲线 $y^2=4x^3-x=x(2x-1)(2x+1)$, 这里 $x,y\in\mathbb{R}$. $\Delta=-16\bigl(4\cdot(-1)^3+27\cdot 0^2\bigr)=64>0$, 因此有两个连通分支. 其函数图像如下

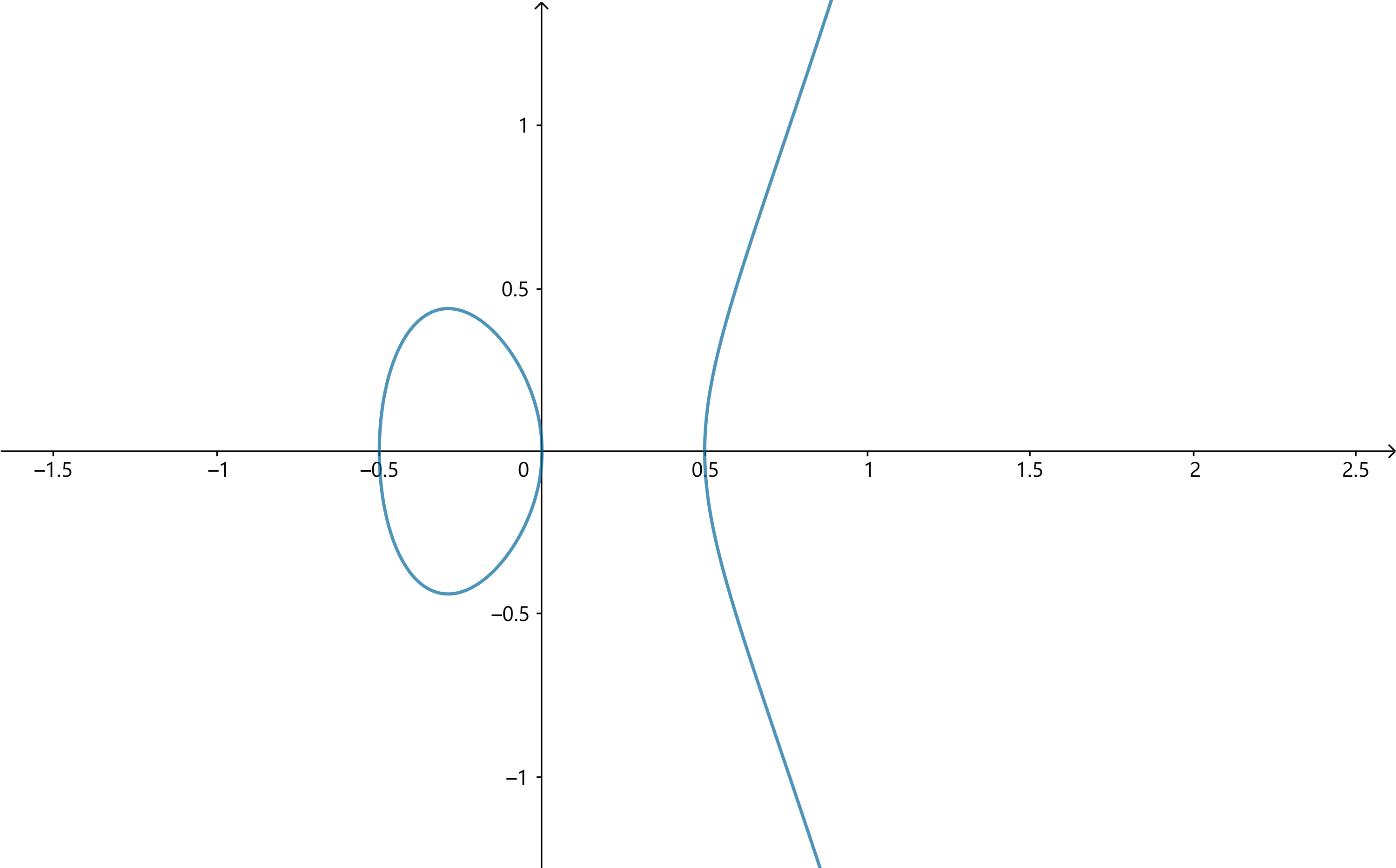
将右侧的曲线加上无穷远点, 则得到两个圆. 现在将这个函数中的变量 $x,y$ 视为复数, 不妨改记为 $z$ 和 $w$. 此时上面这个方程变为
\[
w^2=z(2z-1)(2z+1).
\]
这定义了一个复椭圆曲线, 证明其拓扑(在添加一无穷远点后)正好是一个环面(torus).

更准确地说, 我们应该能够将平面平铺成大小相等的平行四边形（称为周期平行四边形或基本平行四边形）, 这样每个图块上的图形部分是相同的.

以上翻译自 [1]

References:

[1] https://www.math.purdue.edu/~arapura/graph/elliptic.html