of {$slidecount} ½ {$title}, {$author}

首页






Lusin 定理的证明
— 实分析和复分析 —


Haifeng Xu


(hfxu@yzu.edu.cn)

2021-07-03

此课件基于 W. Rudin 所著《实分析和复分析》

目录

内容

内容

由于连续函数在 Borel 测度、特别在 Lebesgue 测度的结构中占有如此突出的地位, 似乎有理由相信在连续函数和可测函数之间会存在着某些有趣的联系.

由于可测函数从定义上就和拓扑是有联系的. 某种程度上, 可测集“对应了”开集, $\sigma$-代数“对应着”拓扑(当然, 它们是有区别的, 性质也不完全有类比性). 可测函数和连续函数之间肯定有一些联系. 平凡性质例如: 可测函数的连续函数是可测的.($h=g\circ f$, $f$ 可测, $g$ 连续, 则可推测 $h$ 可测.)

这里介绍的 Lusin 定理, 描述了可测函数可以由 $X$ 上具有紧支集的连续函数逼近. 从而更好地理解可测函数的结构.

另一个 Vitali-Carathéodory 定理描述的是 $X$ 上的实值 $L^1$ $\mu$-可积函数可以被两个半连续函数从积分上逼近.

 

Lusin 简介

Lusin 简介

Lusin 现在写为 Luzin. 很多书中还是保留了以前的写法.

Lusin (Никола́й Никола́евич Лу́зин) (1883--1950)是苏联数学家, 莫斯科大学教授.

Lusin 是莫斯科数学学院的创始人. 他的学生中有

A. N. Kolmogorov

参考

 

基本概念之回顾

基本概念之回顾

拓扑

定义(开集公理). 设 $X$ 是非空集合, $\tau\subset\mathscr{P}(X)$. 如果 $\tau$ 满足下列条件:
(1) $X,\emptyset\in\tau$.
(2) $G_1, G_2\in\tau\ \Rightarrow\ G_1\cap G_2\in\tau$.
(3) $\{G_{\lambda}\}_{\lambda\in\Lambda}\subset\tau$, $(\Lambda\neq\emptyset)$ $\Rightarrow\ \cup_{\lambda\in\Lambda}G_{\lambda}\in\tau$.
则称 $\tau$ 是 $X$ 的一个拓扑. $\langle X,\tau\rangle$ 称为拓扑空间. $\tau$ 的每个成员叫做 $X$ 的 $\tau$-开集.

$\tau$-开集的补集叫做 $X$ 的 $\tau$-闭集. (在不引起混淆时, 在讲开集闭集时, 所基于的拓扑 $\tau$ 可省略.)

我们用 $A^c$ 表示 $A$ 在 $X$ 中的补集.

定理. 设 $\langle X,\tau\rangle$ 为拓扑空间, 则有
(1) $\emptyset$, $X$ 都是 $X$ 的闭集.
(2) $X$ 的任意两个闭集的并是 $X$ 的闭集.
(3) $X$ 的任意多个闭集的交是 $X$ 的闭集.

$\sigma$-代数

定义. 集 $X$ 的子集族 $\mathfrak{M}$ 称为 $X$ 的一个 $\sigma$-代数, 若 $\mathfrak{M}$ 具有如下性质:
(i) $X\in\mathfrak{M}$.
(ii) 若 $A\in\mathfrak{M}$, 则 $A^c\in\mathfrak{M}$.
(iii) 若 $A=\cup_{n=1}^{\infty}A_n$, 且 $A_n\in\mathfrak{M}$, $n=1,2,3,\ldots$, 则 $A\in\mathfrak{M}$.

$\sigma$-代数中 $\sigma$ 体现在 $\cup_{n=1}^{\infty}$.

可测空间与可测集

定义. 若 $\mathfrak{M}$ 是 $X$ 的一个 $\sigma$-代数, 则称 $X$ 为可测空间. 且 $\mathfrak{M}$ 的元素称为可测集.

可测函数

定义. 设 $f:X\rightarrow Y$ 是可测空间 $(X,\mathfrak{M})$ 到拓扑空间 $\langle Y,\tau_Y\rangle$ 的一个映射. 若对每个 $V\in\tau_Y$, $f^{-1}(V)\in\mathfrak{M}$, 则称 $f$ 是可测的(measurable).

也即, 若每个开集的原像是可测集, 则映射 $f$ 称为可测函数.

简单函数及其表示

定义. 设 $s: X\rightarrow[0,\infty)$ 是可测空间 $(X,\mathfrak{M})$ 上的函数. $s$ 的值域仅由 $[0,\infty)$ 内有限个点组成, 则称 $s$ 为 简单函数(simple function/step function).

如果 $s$ 的值域为 $\{\alpha_1,\alpha_2,\ldots,\alpha_n\}$, 令 \[ A_i=\{x\mid s(x)=\alpha_i\},\quad i=1,2,\ldots,n. \] 则 \[ s=\sum_{i=1}^{n}\alpha_i\cdot\chi_{_{A_i}}. \]

命题. $s$ 是可测函数当且仅当每个 $A_i$ 是可测集.

思考. 可测函数为何定义为可测空间到拓扑空间的映射, 而不是拓扑空间到可测空间的映射?

注意, 拓扑空间总是可以成为一个可测空间. 因为 $\langle X,\tau\rangle$ 存在一个包含 $\tau$ 的最小的 $\sigma$-代数 $\mathscr{B}$. 我们将 $\mathscr{B}$ 中的元素称为 Borel 集.

若令 $\Omega=\{E\subset Y\mid f^{-1}(E)\in\mathfrak{M}\}$, 则 $\Omega$ 为 $Y$ 内的 $\sigma$-代数.

利用 $f^{-1}$ 的性质很容易证明. 例如: $f^{-1}(E^c)=X-f^{-1}(E)$, 由于 $E\in\Omega$, 故 $f^{-1}(E)\in\mathfrak{M}$, 从而 $X-f^{-1}(E)\in\mathfrak{M}$. 于是根据 $\Omega$ 的定义, $E^c\in\Omega$.

 

测度

测度

正测度

正测度是指满足可数可加性的函数 $\mu: (X,\mathfrak{M})\rightarrow[0,\infty]$. 其中 $\mathfrak{M}$ 是 $X$ 上的 $\sigma$-代数.

所谓的可数可加是指: 若 $\{A_i\}_{i=1}^{\infty}$ 为 $\mathfrak{M}$ 中互不相交的可数集族, 则 \[ \mu\Bigl(\bigcup_{i=1}^{\infty}A_i\Bigr)=\sum_{i=1}^{\infty}\mu(A_i) \]

为避免麻烦, 我们假设至少对一个 $A\in\mathfrak{M}$, $\mu(A) < \infty$.

测度空间

测度空间是一个可测空间 $(X,\mathfrak{M})$ 具有定义在其可测集的 $\sigma$-代数上的正测度, 也即三元有序组 $(X,\mathfrak{M},\mu)$.

复测度

复测度是定义在一个 $\sigma$-代数上的复值可数可加函数. 即 $\mu: (X,\mathfrak{M})\rightarrow\mathbb{C}$.

Borel 测度

定义. 定义在局部紧的 Hausdorff 空间 $X$ 的全体 Borel 集所成 $\sigma$-代数上的测度 $\mu$ 称为 $X$ 上的 Borel 测度.

如果 $\mu$ 满足 \[ \mu(E)=\inf\{\mu(V)\mid E\subset V, V\text{是开集}\},\quad\forall\ E\in\mathfrak{M} \] 则称 $\mu$ 是外正则的.

如果对每个开集 $E$ 和每个 $E\in\mathfrak{M}$ 且 $\mu(E) < \infty$, $\mu$ 满足 \[ \mu(E)=\sup\{\mu(K)\mid K\subset E, K\text{是紧集}\}, \] 则称 $\mu$ 是内正则的.

如果 $X$ 内的每个 Borel 集同时是外正则和内正则的, 则称 $\mu$ 是正则的.

 

局部紧 Hausdorff 空间上的测度

局部紧 Hausdorff 空间上的测度

设 $\mu$ 是局部紧 Hausdorff 空间 $X$ 上的一个测度, 满足下面的性质.

定理. 设 $X$ 是局部紧的 Hausdorff 空间, $\Lambda$ 是 $C_c(X)$ 上的正线性泛函. 则在 $X$ 内存在一个包含 $X$ 的一切 Borel 集的 $\sigma$-代数 $\mathfrak{M}$, 并存在 $\mathfrak{M}$ 上的唯一一个正测度 $\mu$. $\mu$ 在下述意义上表示了 $\Lambda$:

最后一个性质说明 $(X,\mathfrak{M},\mu)$ 是一个完备的测度空间.

相关概念

定义(Hausdorff 空间, 也称 $T_2$ 空间). $\forall\ x,y\in X$, 且 $x\neq y$, $\exists\ U\in\mathcal{N}(x)$, $V\in\mathcal{N}(y)$, s.t. $U\cap V=\emptyset$.

定义(局部紧). 如果拓扑空间 $X$ 的每一点都有一个紧致邻域, 则称 $X$ 是局部紧的.

定理. Hausdorff 空间 $\langle X,\tau\rangle$ 是局部紧的, 当且仅当 $\forall\ x\in X$, $\exists U\in\mathscr{N}(x)\cap\tau$, 使得 $\overline{U}$ 是紧致的.

定理. 若 $\mathscr{F}$ 为 $X$ 的任意子集族, 则在 $X$ 内存在一最小的 $\sigma$-代数 $\mathfrak{M}^*$, 使得 $\mathscr{F}\subset\mathfrak{M}^*$.

称 $\mathfrak{M}^*$ 为由 $\mathscr{F}$ 生成的 $\sigma$-代数.

特别的,

定义 . 设 $\langle X,\tau\rangle$ 是拓扑空间. 则 $X$ 内存在一个最小的 $\sigma$-代数 $\mathscr{B}$, 使得 $X$ 内每一个开集都属于 $\mathscr{B}$. (即, $\forall\ U\in\tau$, $U\in\mathscr{B}$). 称 $\mathscr{B}$ 中的元素为 $X$ 的Borel 集.

性质

定理. 拓扑空间 $X$ 的一点紧化 $X^*$ 是 Hausdorff 的, 当且仅当 $X$ 是局部紧的 Hausdorff 空间.

推论. 如果 $X$ 是局部紧的 Hausdorff 空间, 那么 $X$ 是完全正则的 $T_1$ 空间, 即 Tychonoff 空间.

以上性质参考自 [1] 定理 5.7.3 及推论 5.7.4.

  1. 陆文钊、陈肇姜 编《点集拓扑学》, 南京大学出版社, 1995.

 

常用的一个区间分解

常用的一个区间分解

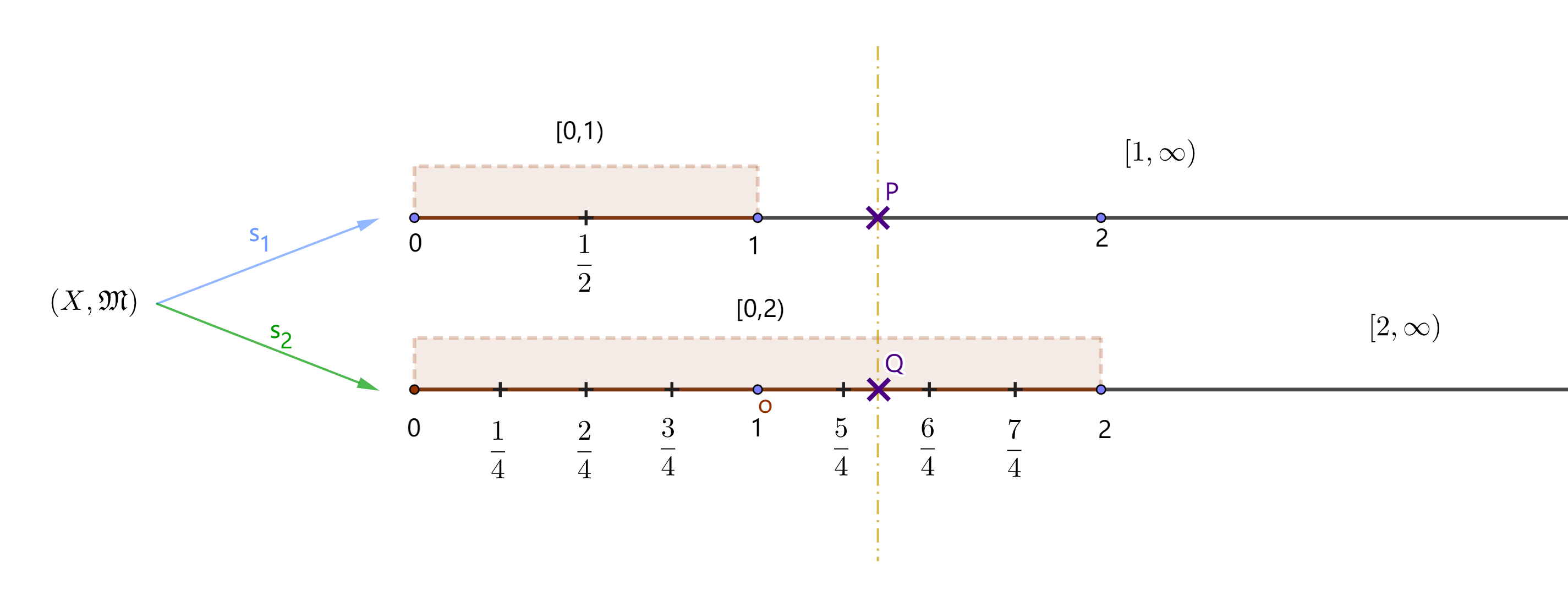
\[[0,\infty]=[0,n)\cup[n,\infty]\]

将 $[0,n)$ 分成 $n2^n$ 个左闭右开的等长小区间, 每个小区间长度为 $\frac{1}{2^n}$. 即 \[ [0,n)=[0,\frac{1}{2^n})\cup[\frac{2-1}{2^n},\frac{2}{2^n})\cup[\frac{3-1}{2^n},\frac{3}{2^n})\cup\cdots\cup[\frac{n2^n-1}{2^n},\frac{n2^n}{2^n}) \]

可测函数原像集

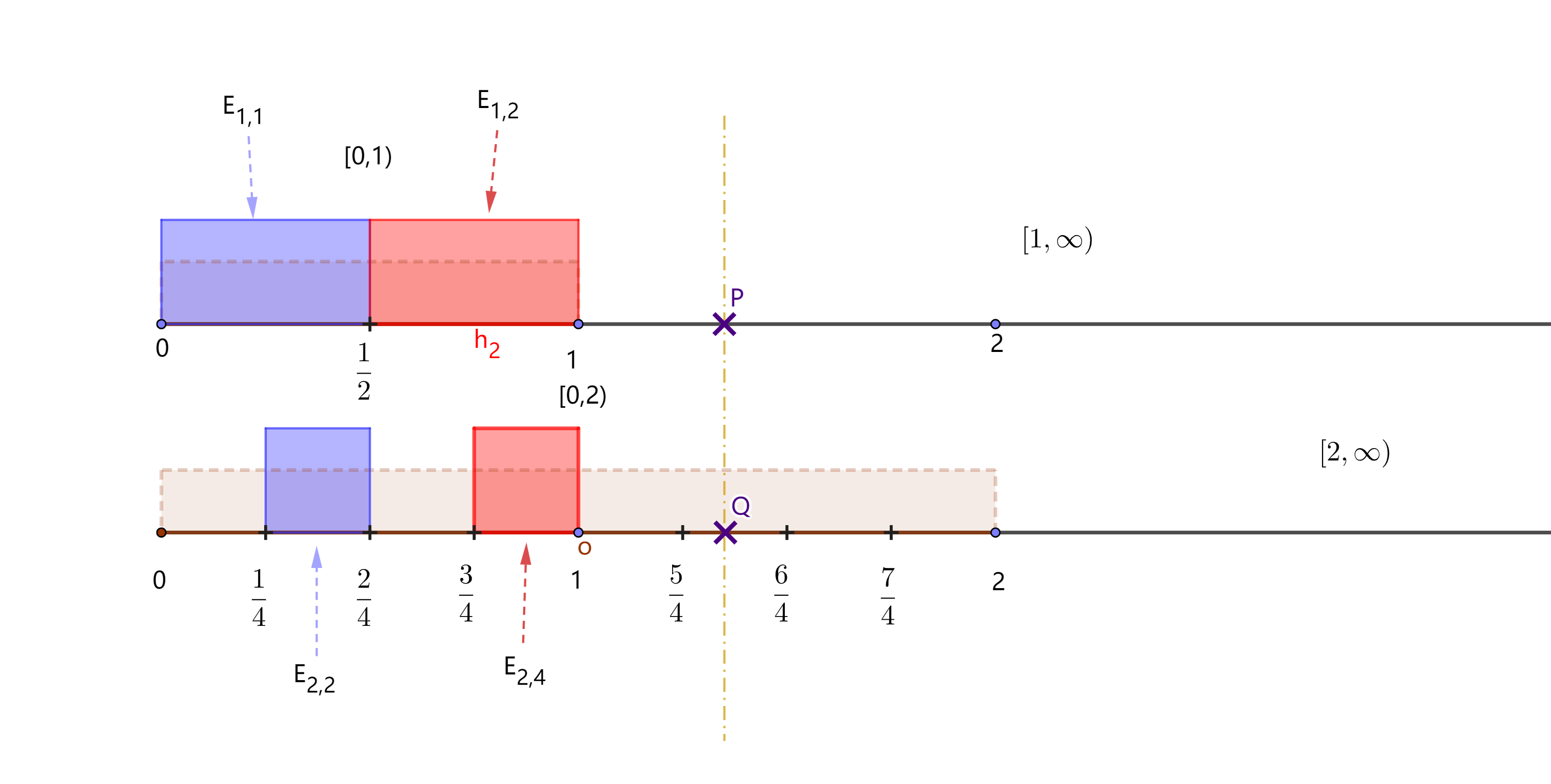
设 $f:X\rightarrow[0,\infty]$ 可测. $[0,\infty]$ 按上面方式拆分. 定义 \[ \begin{aligned} E_{n,i}&=f^{-1}\Bigl(\Bigl[\frac{i-1}{2^n},\frac{i}{2^n}\Bigr)\Bigr),\quad i=1,2,3,\ldots,n2^n.\\ F_n&=f^{-1}([n,\infty]). \end{aligned} \]

并且令 \[ s_n=\sum_{i=1}^{n2^n}\frac{i-1}{2^n}\chi_{_{E_{n,i}}}+n\chi_{_{F_n}}. \]

由下面的定理, $E_{n,i}$ 及 $F_n$ 均为可测集.

定理. 假设 $\mathfrak{M}$ 是 $X$ 内的 $\sigma$-代数, $Y$ 为拓扑空间, $f$ 映 $X$ 到 $Y$ 内:

 

可测函数可由简单函数逼近

可测函数可由简单函数逼近

定理. 设 $f:X\rightarrow[0,\infty]$ 可测. 则存在 $X$ 上的简单可测函数 $s_n$ 使得

证明. $s_n$ 如前面所定义. \[ s_n=\sum_{i=1}^{n2^n}\frac{i-1}{2^n}\chi_{_{E_{n,i}}}+n\chi_{_{F_n}}. \]

(1) 若 $x\in E_{n,i}$, 则 $\exists\ y\in[\frac{i-1}{2^n},\frac{i}{2^n})$, s.t. $f^{-1}(y)=x$, 即 $y=f(x)$. $s_n(x)=\frac{i-1}{2^n}$, 故 $s_n(x)\leqslant y=f(x)$, 对任意 $n$ 都成立.

(2) 若 $x\in F_n$, 则 $\exists\ y\in[n,\infty]$, s.t. $f^{-1}(y)=x$. \[ s_n(x)=n\leqslant y=f(x). \]

因此, $s_n\leqslant f$ 对 $n=1,2,3,\ldots$ 都成立.

$s_n\leqslant s_{n+1}$ 可从其定义看出. 我们以 $s_1\leqslant s_2$ 为例.

\[ s_1=\sum_{i=1}^{2}\frac{i-1}{2}\chi_{_{E_{1,i}}}+1\cdot\chi_{_{F_1}} \]

\[ s_2=\sum_{i=1}^{2\cdot 2^2}\frac{i-1}{2^2}\chi_{_{E_{2,i}}}+2\cdot\chi_{_{F_2}} \]

(a) 若 $f(x)\in[2,\infty]$, 则 $s_1(x)=\chi_{_{F_1}}(x)=1$. 而 $s_2(x)=2\chi_{_{F_2}}(x)=2$. 故 $s_1(x)\leqslant s_2(x)$ 成立.

(b) 若 $f(x)\in[1,2)$, 则 $s_1(x)=\chi_{_{F_1}}(x)=1$. 另一方面, $x\in E_{2,k}$, 这里 $\frac{k-1}{2^2}\geqslant 1$, 即 $k\geqslant 4+1=5$. 从而 \[ s_2(x)=\frac{k-1}{2^2}\chi_{_{E_{2,k}}}(x) \geqslant \frac{5-1}{4}=1 \]

(c) 若 $f(x)\in[0,1)$, 分情况类似证明. (i) 若 $f(x)\in[0,\frac{1}{2})$, $x\in E_{1,1}=f^{-1}\Bigl([\frac{0}{2^1},\frac{1}{2^1})\Bigr)$. 此时 \[ s_1(x)=\frac{1-1}{2^1}\chi_{_{E_{1,1}}}=0. \] 从而 $s_1(x)\leqslant s_2(x)$ 成立. (ii) 若 $f(x)\in[\frac{1}{2},1)$, $x\in E_{1,2}=f^{-1}\Bigl([\frac{2-1}{2^1},\frac{2}{2^1})\Bigr)$. 此时 \[ s_1(x)=\frac{2-1}{2^1}\chi_{_{E_{1,2}}}=\frac{1}{2}. \] 此时, $x$ 在某个 $E_{2,k}$ 中, $E_{2,k}=f^{-1}\Bigl([\frac{k-1}{2^2},\frac{k}{2^2})\Bigr)$. 故 $\frac{k-1}{2^2}\geqslant\frac{2}{2^2}$, 即 $k\geqslant 3$. 从而 \[ s_2(x)=\frac{k-1}{2^2}\chi_{_{E_{2,k}}}\geqslant\frac{2}{2^2}=\frac{1}{2}=s_{1}(x). \]

一般情况也类似证明, 此即 (a).

若 $x$ 使得 $f(x) < \infty$, 则当 $n$ 足够大时, \[ s_n\geqslant f(x)-\frac{1}{2^n} \]

若 $x$ 使得 $f(x)=\infty$, 则 $s_n(x)=n$.

这就证明了 (b).

简单函数的重要性

从简单函数的积分可以定义可测函数的 Lebesgue 积分.

应用

这里构造的简单函数列在很多定理的证明中有用到. 比如 Lebesgue 单调收敛定理, 可测函数项级数的积分定理等等.

 

Lusin Theorem

Lusin 定理

Lusin 定理. 设 $f:X\rightarrow\mathbb{C}$ 是复可测函数, $A\subset X$, 且 $\mu(A) < \infty$, 如果 $x\not\in A$, $f(x)=0$, 并且 $\varepsilon>0$. 则存在一个 $g\in C_c(X)$, 使得 \[ \mu(\{x\ :\ f(x)\neq g(x)\}) < \varepsilon.\tag{1} \] 并且, 还可以做到 \[ \sup_{x\in X}|g(x)|\leqslant\sup_{x\in X}|f(x)|.\tag{2} \]

证明. 首先假设 $f$ 是有界的实值函数, $0\leqslant f < 1$, 并且 $A$ 是紧的. 如之前, 作出一个收敛于 $f$ 的序列 $\{s_n\}$. 具体的, 令 \[ s_n=\sum_{i=1}^{n2^n}\frac{i-1}{2^n}\chi_{E_{n,i}}. \]

注意, 由于 $0\leqslant f < 1$, 故最后一项 $n\chi_{_{F_n}}(x)$ 去掉了.

令 $t_1=s_1$, $t_n=s_n-s_{n-1}$, $n=2,3,4,\ldots$

则 $2^n t_n$ 是集 $T_n\subset A$ 的特征函数, 而且 \[ f(x)=\sum_{n=1}^{\infty}t_n(x)\qquad (x\in X)\tag{3} \] 这里 \[ \begin{split} T_n&=\{x\in A\mid t_n(x)=\frac{1}{2^n}\}\\ &=\{x\in E_{n,i}\cap E_{n-1,j}\mid (i-1)-2(j-1)=1\ \text{即}\ i=2j\} \end{split} \]

\[ 2^n t_n=\sum_{i=1}^{n2^n}(i-1)\chi_{_{E_{n,i}}}-\sum_{j=1}^{(n-1)2^{n-1}}2(j-1)\chi_{_{E_{n-1,j}}} \] 若 $x\in E_{n,i}\cap E_{n-1,j}$ 满足 $t_n(x)=\frac{1}{2^n}$, 则 \[ (i-1)\chi_{_{E_{n,i}}}-2(j-1)\chi_{_{E_{n-1,j}}}=1, \] 即 \[ (i-1)-2(j-1)=1\quad\Rightarrow\quad i=2j. \]

固定开集 $V$ 使得 $A\subset V$, 而且 $\overline{V}$ 是紧的. 则存在紧集 $K_n$ 和开集 $V_n$ 使得 $K_n\subset T_n\subset V_n\subset V$ 且 $\mu(V_n-K_n) < \frac{\varepsilon}{2^n}$. 由 Urysohn 引理, 存在函数 $h_n$ 使得 $K_n\prec h_n\prec V_n$. ($\sum_{n}h_n=1$, by 单位分解定理.)

定义 \[g(x)=\sum_{n=1}^{\infty}\frac{1}{2^n}h_n(x)\quad (x\in X)\tag{4}\]

这个级数在 $X$ 上一致收敛, 因而 $g$ 是连续的. 并且, $g$ 的支集含于 $\overline{V}$ 中.

由于除开在 $V_n-K_n$ 中以外, $2^{-n}h_n(x)=t_n(x)$, 所以除开在 $\cup(V_n-K_n)$ 中以外, $g(x)=f(x)$, 并且后一个集有比 $\varepsilon$ 小的测度. 这样, 当 $A$ 是紧的, $0\leqslant f < 1$ 时, (1) 式成立.

由此得到, 当 $A$ 是紧的, $f$ 是有界可测函数时, (1) 式成立.

$A$ 的紧性容易去掉, 因为, 如果 $\mu(A) < \infty$, 则 $A$ 包含一个紧集 $K$, 使得 $\mu(A-K)$ 小于事先给定的任意正数. 再者, 如果 $f$ 是个复可测函数, $B_n=\{x\ :\ |f(x)| > n\}$, 则 $\cap B_n=\emptyset$, 于是由之前的定理, $\mu(B_n)\rightarrow 0$. 由于除开在 $B_n$ 上以外, $f$ 同有界函数 $(1-\chi_{B_n})\cdot f$ 一致, 故在一般情形下 (1) 也成立.

最后, 令 $R=\sup\{|f(x)|\ :\ x\in X\}$, 并定义, \[ \varphi(z)=\begin{cases} z, & |z|\leqslant R,\\ \frac{Rz}{|z|}, & |z| > R, \end{cases} \]

则 $\varphi$ 是复平面到半径为 $R$ 的圆盘上的连续映射. 如果 $g$ 满足 (1), $g_1=\varphi\circ g$, 则 $g_1$ 满足 (1) 和 (2).

 

推论

推论

推论. 设满足 Lusin 定理的条件, 且 $|f|\leqslant 1$, 则存在序列 $\{g_n\}$, 使得 $g_n\in C_c(X)$, $|g_n|\leqslant 1$, 且 \[f(x)=\lim_{n\rightarrow\infty}g_n(x)\qquad\text{a.e.}\tag{5}\]

证明. 由 Lusin 定理得出, 令 $\varepsilon_n=\frac{1}{2^n}$, 对每个 $n$ 对应有一个 $g_n\in C_c(X)$, 而 $|g_n|\leqslant 1$, 使得 $\mu(E_n)\leqslant 2^{-n}$.

这里 \[ E_n=\{x\in X\mid f(x)\neq g_n(x)\}. \] 因为 \[ \mu(\bigcap_{n=1}^{\infty}E_n)=0, \] 故对几乎每个 $x\in X$, 它至多属于有限多个集 $E_n$. 对任意一个这样的 $x$ 和充分大的 $n$ 都有 $f(x)=g_n(x)$. 这就得到 (5).

 

Vitali-Carathéodory 定理

Vitali-Carathéodory 定理

定理(Vitali-Carathéodory). 设 $f\in L^1(\mu)$, $f$ 是实值的, 并且 $\varepsilon > 0$. 则在 $X$ 上存在函数 $u$ 和 $v$ 使得 $u\leqslant f\leqslant v$, $u$ 是上半连续且有上界, $v$ 是下半连续且有下界, 且 \[ \int_X(v-u)\mathrm{d}\mu < \varepsilon.\tag{1} \]

证明

首先假定 $f\geqslant 0$, 并且 $f$ 不恒等于 $0$. (如果 $f\equiv 0$, 则取 $u=v\equiv 0$ 即可.)

由于 $f$ 是一个简单函数 $s_n$ 的递增序列的点态极限, $f$ 就是简单函数 $t_n=s_n-s_{n-1}$ (取 $s_0=0$)的和.

再由于 $t_n$ 是特征函数的线性组合, 就存在可测集 $E_i$ (不一定要互不相交)和常数 $c_i > 0$, 使得

\[ f(x)=\sum_{i=1}^{\infty}c_i\chi_{_{E_i}}(x)\qquad(x\in X)\tag{2} \]

两边取 $X$ 上的 Lebesgue 积分, 得 \[ \int_X f\mathrm{d}\mu=\sum_{i=1}^{\infty}c_i\mu(E_i).\tag{3} \]

由于 $f\in L^{1}(\mu)$, 故级数 $\sum_{i=1}^{\infty}c_i\mu(E_i)$ 收敛.

存在紧集 $K_i$ 和开集 $V_i$, 使得 $K_i\subset E_i\subset V_i$, 且 \[ c_i\mu(V_i-K_i) < \frac{\varepsilon}{2^{i+1}}\qquad(i=1,2,3,\ldots)\tag{4} \]

令 \[ v=\sum_{i=1}^{\infty}c_i\chi_{_{V_i}},\qquad u=\sum_{i=1}^{N}c_i\chi_{_{K_i}},\tag{5} \]

其中 $N$ 是这样选择得, 使得 \[ \sum_{i=N+1}^{\infty}c_i\chi_{_{E_i}} < \frac{\varepsilon}{2}.\tag{6} \]

根据 $v$ 和 $u$ 的构造, $v$ 是下半连续的, $u$ 是上半连续的, $u\leqslant f\leqslant v$.

并且, \[ \begin{split} v-u&=\sum_{i=1}^{N}c_i(\chi_{_{V_i}}-\chi_{_{K_i}})+\sum_{i=N+1}^{\infty}\chi_{_{V_i}}\\ &\leqslant\sum_{i=1}^{\infty}c_i(\chi_{_{V_i}}-\chi_{_{K_i}})+\sum_{i=N+1}^{\infty}\chi_{_{E_i}}. \end{split} \]

(这里 $\leqslant$ 是因为 $\chi_{_{V_i}}-\chi_{_{E_i}}\leqslant\chi_{_{V_i}}-\chi_{_{K_i}}$.)

两边在 $X$ 上取积分, 由 (4) 和 (6) 即得 $\displaystyle\int_X(v-u)\mathrm{d}\mu < \varepsilon$.

在一般情况下, 记 $f=f^{+}-f^{-}$. 如上一样, 对 $f^{+}$ 作出 $u_1$ 和 $v_1$, 对 $f^{-}$ 作出 $u_2$ 和 $v_2$, 于是有 \[ \begin{cases} u_1&\leqslant f^{+}\leqslant v_1\\ u_2&\leqslant f^{-}\leqslant v_2\\ \end{cases}\quad\Rightarrow\quad \begin{cases} u_1&\leqslant f^{+}\leqslant v_1\\ -v_2&\leqslant -f^{-}\leqslant -u_2\\ \end{cases} \]

两式相加, 得 \[ u_1-v_2\leqslant f^{+}-f^{-}\leqslant v_1-u_2 \]

令 $u=u_1-v_2$, $v=v_1-u_2$. 这里 $v_i$ 是下半连续的, 故 $-v_i$ 是上半连续的. 两个上半连续函数的和仍为上半连续, 故 $u$ 是上半连续的. 类似可证 $v$ 是下半连续的. 故 $u$ 和 $v$ 符合要求.

解释

可列个下半连续函数的和仍是下半连续的; 有限个上半连续的和还是上半连续的. (参见问题1220)

 

End






Thanks!