二项树的堆序
二项树的堆序
如果我们把堆序施加到二项树上并允许任意高度上最多一棵二项树, 那么我们能够用二项树的集合唯一地表示任意大小的优先队列.
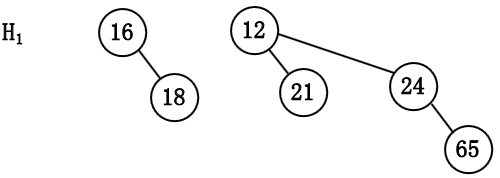
例如, 大小为 13 的优先队列可以用森林
作为例子, 6 个元素的优先队列可以表示为如下形状.
This slide is based on the book of Mark Allen Weiss
张怀勇等译.
打印机的作业一般都放在队列中.
在多用户环境中, 操作系统调度程序必须决定在若干进程中运行那个进程.
为实现这类特殊的应用, 我们需要一种称之为
优先队列还被用于排序中. 在
优先队列是至少允许下列两种操作的数据结构:
C++ 提供两种版本的 deleteMin. 一个是删除最小项, 另一个在删除最小项的同时在通过引用传递的对象中存储所删掉的值.
其他操作是扩展的操作.
基于
对于第三种实现, 由于删除操作删除的是最小元, 反复除去左子树中的结点似乎损害了树的平衡, 使得右子树加重.
然而右子树是随机的. 在最坏情形, 即 deleteMin 将左子树删空的情形下, 右子树拥有的元素最多也就是它应具有的两倍. 这只是在其期望的深度上加了一个小常数.
注意, 通过使用平衡树, 可以把界变成最坏情形的界; 这将防止出现不好的插入序列.
使用查找树也有缺点, 查找树有大量并不需要的操作.
我们将要使用的基本数据结构不需要链, 它以最坏情形时间
插入实际上将花费常数平均时间, 若无删除干扰, 该结构的实现将以线性时间建立一个具有
我们还将讨论如何实现优先队列以支持有效的合并, 这个附加的操作需要使用链接的结构.
这里我们将二叉堆简称
与二叉查找树一样, 堆也有两个性质, 即
类似于 AVL 树, 对堆的操作可能破坏其中一个性质, 因此, 堆的操作必须到堆的所有性质都被满足时才能终止.
堆是一棵完全填满的二叉树, 可能的例外是在底层, 底层上的元素从左到右填入. 这样的二叉树我们称为
作为 Exercise, 可使用归纳法证明.
通过观察, 发现完全二叉树可以使用数组实现而不必使用链表, 原因在于
(2) 结点
因此, 这里不需要链, 而且遍历该树所需要的操作也极简单.
这种实现方法的唯一问题在于, 堆的大小事先需要估计. 但一般情况下这并不成问题. 而且如果需要, 我们可以重新调整.
因此, 一个堆数据结构由一个(Comparable 对象的)数组和一个代表当前堆大小的整数组成.
template <typename Comparable>
class BinaryHeap
{
public:
explicit BinaryHeap( int capacity = 100 );
explicit BinaryHeap( const vector & items );
bool isEmpty( ) const;
const Comparable & findMin( ) const;
void insert( const Comparable & x );
void deleteMin( );
void deleteMin( Comparable & minItem );
void makeEmpty( );
private:
int currentSize; // Number of elements in heap
vector<Comparable> array; // The heap array
void buildHeap( );
void percolateDown( int hole );
};
由于想要快速找出最小元, 因此最小元应该在根上. 因此
如果考虑任意子树也应该是堆, 那么任意结点就应该小于它的所有后裔.
/**
* Insert item x, allowing duplicates.
*/
void insert( const Comparable & x )
{
if( currentSize == array.size( ) - 1 )
array.resize( array.size( ) * 2 );
// Percolate up
int hole = ++currentSize;
for( ; hole > 1 && x < array[ hole / 2 ]; hole /= 2 )
array[ hole ] = array[ hole / 2 ];
array[ hole ] = x;
}
/**
* Remove the minimum item.
* Throws UnderflowException if empty.
*/
void deleteMin( )
{
if( isEmpty( ) )
throw UnderflowException( );
array[ 1 ] = array[ currentSize-- ];
percolateDown( 1 );
}
/**
* Remove the minimum item and place it in minItem.
* Throws UnderflowException if empty.
*/
void deleteMin( Comparable & minItem )
{
if( isEmpty( ) )
throw UnderflowException( );
minItem = array[ 1 ];
array[ 1 ] = array[ currentSize-- ];
percolateDown( 1 );
}
/**
* Internal method to percolate down in the heap.
* hole is the index at which the percolate begins.
*/
void percolateDown( int hole )
{
int child;
Comparable tmp = array[ hole ];
for( ; hole * 2 <= currentSize; hole = child )
{
child = hole * 2;
if( child != currentSize && array[ child + 1 ] < array[ child ] )
child++;
if( array[ child ] < tmp )
array[ hole ] = array[ child ];
else
break;
}
array[ hole ] = tmp;
}
explicit BinaryHeap( const vector & items )
: array( items.size( ) + 10 ), currentSize( items.size( ) )
{
for( int i = 0; i < items.size( ); i++ )
array[ i + 1 ] = items[ i ];
buildHeap( );
}
/**
* Establish heap order property from an arbitrary
* arrangement of items. Runs in linear time.
*/
void buildHeap( )
{
for( int i = currentSize / 2; i > 0; i-- )
percolateDown( i );
}
注意这里的 buildHeap() 对于 percolateDown 是递减做的. 请实验一下, 如果 i 递增会怎样? (经过循环后可能仍然不是一个堆.)
虽然求最小值操作可以在常数时间完成, 但是, 按照求最小元设计的堆(也称
事实上, 一个堆所蕴涵的关于序的信息很少, 因此, 若不对整个堆进行线性搜索, 是没有办法找出任何特定的元素的.
对于最小堆, 最大元必定出现在叶子上, 不过叶子的数目是总的结点数的一半以上.
Exercise, 计算
设有 $N$ 个数 $\{a_1,a_2,\ldots, a_N\}$, 确定其中第 $k$ 大的数.
注意第 1 大的数也就是最大元.
构造堆的最坏情形是 $O(N)$ 时间, 每次执行 deleteMin 是 $O(\log N)$ 时间. 由于执行了 $k$ 次 deleteMin 操作, 因此我们得到总的运行时间为 $O(N+k\log N)$. 如果 $k=O(\frac{N}{\log N})$, 那么运行时间为 $O(N)$, 相当于取决于 buildHeap 操作. 对于大的 $k$, 运行时间为 $O(k\log N)$. 如果 $k=[N/2]$, 则运行时间为 $\Theta(N\log N)$.
特别的, 令 $k=N$, 运行该程序并在元素离开堆时记录下这些元素的值, 那么实际上就是对输入文件以时间 $O(N\log N)$ 进行了排序. 在第七章, 我们将细化该想法, 并得到一种快速的排序算法, 称为
我们使用算法 1.B 的思路. 在任一时刻都将维持 $k$ 个元素的集合 $S$. 不过这里使用一个堆来实现 $S$.
因此, 总的运行时间是 $O(k+(N-k)\log k)=O(N\log k)$. 该算法对于找出中位数, 也给出了时间界 $O(N\log N)$.
$d$ 堆是二叉堆的推广, 它的所有结点都有 $d$ 个儿子.
$d$ 堆要比二叉堆浅得多, 它将 insert 操作的运行时间改进为 $O(\log_d N)$.
但是对于大的 $d$, deleteMin 操作就费时得多. 虽然树浅了, 但是必须要找出 $d$ 个儿子中最小的一个.
现在找出儿子和父亲的乘法和除法都有个因子 $d$, 因此除非 $d$ 是 $2$ 的幂, 否则将会由于不能通过二进制移位来实现除法而导致运行时间的急剧增加.
$d$ 堆在理论上很有趣, 因为存在许多算法, 其插入次数比 deleteMin 的次数多很多, 因此理论上的加速是可能的.
当优先队列太大不能完全装入主存时, $d$ 堆也是很有用的. 在这种情况下, $d$ 堆可以与 $B$ 树大致相同的方式发挥作用.
有证据显示, 在实践中, $4$ 堆可以胜过二叉堆.
除了不能执行
我们将这个操作称为
有许多实现堆的方法可以是一次
下面讨论三种复杂程度不一的数据结构, 它们都有效地支持 merge 操作.
所有支持有效合并的高级数据结构都需要使用链式数据结构. 实践中, 这可能使得其他操作变慢.
左式堆(也叫左式树 leftist tree, 左偏树)首先是一个二叉树, 它与二叉堆的惟一区别是: 左式堆不是理想平衡的(perfectly balanced), 而且事实上是趋于非常不平衡的.
左式堆与二叉堆一样既有结构性质, 又有堆序性质.
Def: 任一结点
Exer: 给出一个二叉树, 请填写每个结点的零路径长.
对于堆中每一个结点
否则, 就会存在一条更短的路径通过某个结点 $X$ 并取得左儿子, 此时 $X$ 就破坏了左式堆的性质.
证明: (使用归纳法证明) 若
若 $r=2$, 即右路径上有两个结点, 根结点和它的右儿子. 由于是左式堆, 根结点左儿子的零路径长要大于等于右儿子的零路径长, 故必有左儿子. 从而总的结点数至少为 $3=2^2-1$.
设定理对
记根结点的右儿子为 $N_{R1}$, 根结点的左儿子为 $N_{L1}$. 则 $\text{npl}(N_{R1})=k$. 因此 $N_{L1}$ 的零路径长也至少为 $k$. 由于是左式树, 因此 $N_{L1}$ 的右路径至少也有 $k$ 个结点(包括 $N_{L1}$). 根据归纳假设, 根结点的左子树也至少有 $2^k-1$ 个结点. 从而总的结点数至少有 \[ 1+(2^k-1)+(2^k-1)=2^{k+1}-1. \]
从这个定理可以得到, $N$ 个结点的左式树有一条右路径最多含有 $\lfloor\log(N+1)\rfloor$ 个结点.
将所有的工作放到右路径上进行, 它保证路径不会太深.
惟一要注意的是, 对右路径的
左式堆的基本操作是合并.
插入只是合并的特殊情形, 因为可以把插入看成是单结点堆与一个大的堆的
首先我们给出一个简单的递归解法, 然后介绍如何非递归地施行该解法.
template <typename Comparable>
class LeftistHeap
{
public:
LeftistHeap( );
LeftistHeap( const LeftistHeap & rhs );
~LeftistHeap( );
bool isEmpty( ) const;
const Comparable & findMin( ) const;
void insert( const Comparable & x );
void deleteMin( );
void deleteMin( Comparable & minItem );
void makeEmpty( );
void merge( LeftistHeap & rhs );
const LeftistHeap & operator=( const LeftistHeap & rhs );
private:
struct LeftistNode
{
Comparable element;
LeftistNode *left;
LeftistNode *right;
int npl;
LeftistNode( const Comparable & theElement, LeftistNode *lt = NULL,
LeftistNode *rt = NULL, int np = 0 )
: element( theElement ), left( lt ), right( rt ), npl( np ) { }
};
LeftistNode *root;
LeftistNode * merge( LeftistNode *h1, LeftistNode *h2 );
LeftistNode * merge1( LeftistNode *h1, LeftistNode *h2 );
void swapChildren( LeftistNode *t );
void reclaimMemory( LeftistNode *t );
LeftistNode * clone( LeftistNode *t ) const;
};
/**
* Merge rhs into the priority queue.
* rhs becomes empty. rhs must be different from this.
*/
void merge( LeftistHeap & rhs )
{
if( this == &rhs ) // Avoid aliasing problems
return;
root = merge( root, rhs.root );
rhs.root = NULL;
}
/**
* Internal method to merge two roots.
* Deals with deviant cases and calls recursive merge1.
*/
LeftistNode * merge( LeftistNode *h1, LeftistNode *h2 )
{
if( h1 == NULL )
return h2;
if( h2 == NULL )
return h1;
if( h1->element < h2->element )
return merge1( h1, h2 );
else
return merge1( h2, h1 );
}
/**
* Internal method to merge two roots.
* Assumes trees are not empty, and h1's root contains smallest item.
*/
LeftistNode * merge1( LeftistNode *h1, LeftistNode *h2 )
{
if( h1->left == NULL ) // Single node
h1->left = h2; // Other fields in h1 already accurate
else
{
h1->right = merge( h1->right, h2 );
if( h1->left->npl < h1->right->npl )
swapChildren( h1 );
h1->npl = h1->right->npl + 1;
}
return h1;
}
/**
* Inserts x; duplicates allowed.
*/
void insert( const Comparable & x )
{
root = merge( new LeftistNode( x ), root );
}
/**
* Remove the minimum item.
* Throws UnderflowException if empty.
*/
void deleteMin( )
{
if( isEmpty( ) )
throw UnderflowException( );
LeftistNode *oldRoot = root;
root = merge( root->left, root->right );
delete oldRoot;
}
/**
* Remove the minimum item and place it in minItem.
* Throws UnderflowException if empty.
*/
void deleteMin( Comparable & minItem )
{
minItem = findMin( );
deleteMin( );
}
/**
* Find the smallest item in the priority queue.
* Return the smallest item, or throw Underflow if empty.
*/
const Comparable & findMin( ) const
{
if( isEmpty( ) )
throw UnderflowException( );
return root->element;
}
/**
* Returns true if empty, false otherwise.
*/
bool isEmpty( ) const
{ return root == NULL; }
/**
* Make the priority queue logically empty.
*/
void makeEmpty( )
{
reclaimMemory( root );
root = NULL;
}
/**
* Internal method to make the tree empty.
* WARNING: This is prone to running out of stack space;
* exercises suggest a solution.
*/
void reclaimMemory( LeftistNode *t )
{
if( t != NULL )
{
reclaimMemory( t->left );
reclaimMemory( t->right );
delete t;
}
}
/**
* Swaps t's two children.
*/
void swapChildren( LeftistNode *t )
{
LeftistNode *tmp = t->left;
t->left = t->right;
t->right = tmp;
}
const LeftistHeap & operator=( const LeftistHeap & rhs )
{
if( this != &rhs )
{
makeEmpty( );
root = clone( rhs.root );
}
return *this;
}
/**
* Internal method to clone subtree.
* WARNING: This is prone to running out of stack space.
* exercises suggest a solution.
*/
LeftistNode * clone( LeftistNode *t ) const
{
if( t == NULL )
return NULL;
else
return new LeftistNode( t->element, clone( t->left ), clone( t->right ), t->npl );
}
斜堆是是左式堆的自调节形式. 斜堆和左式堆的关系类似于伸展树与 AVL 树之间的关系.
斜堆是具有堆序的二叉树, 但是不存在对树的结构限制.
与左式堆不同, 斜堆不保存任意结点的零路径长.
斜堆的右路径在任何时刻都可以任意长. 因此, 所有操作的最坏情形运行时间均为
与左式堆相同, 斜堆的基本操作也是合并操作. merge 例程也是递归的. 我们执行与以前完全相同的操作, 但有一个例外, 即: 对于左式堆, 我们查看是否左儿子和右儿子满足左式堆的结构性质, 并在不满足该性质时将它们交换. 但对于斜堆, 交换是无条件的, 除右路径上所有结点的最大者不交换它的左右儿子外, 我们都要进行这种交换.
这是因为不断递归调用, 为保证上层结点(每一次的 root 结点)的值最小, 所以右路径中的最大结点必定位于右路径的最后一个. 它一定没有右儿子, 所以不必交换.
虽然左式堆和斜堆都以每次操作花费
因为, 二叉堆以每次操作花费常数时间支持插入.
如果要插入的元素是新的最小元从而一直上滤到根处, 那么这种插入的时间为 $O(\log N)$. 平均来看, 这种上滤终止得要早.
已经证明: 执行一次插入平均需要 2.607 次比较. 因此 insert 将元素平均上移 1.607 层. 所以差不多是 $O(1)$ 时间.
二项队列支持所有这三种操作(合并、插入、deleteMin), 每次操作的最坏情形运行时间为
这里每一棵树都要求是
这里的二项树森林, 要求同一高度的二项树只能有一棵.
因此, 二项树 $B_k$ 由一个带有儿子 $B_0, B_1,\ldots,B_{k-1}$ 的根组成.
如果我们把堆序施加到二项树上并允许任意高度上最多一棵二项树, 那么我们能够用二项树的集合唯一地表示任意大小的优先队列.
例如, 大小为 13 的优先队列可以用森林
作为例子, 6 个元素的优先队列可以表示为如下形状.

最小元可以通过搜索所有树的树根来找出. 由于最多有
另外, 如果我们记住当最小元在其他操作期间变化时更新它, 那么也可保留最小元的信息并以
我们通过例子来说明如何合并.
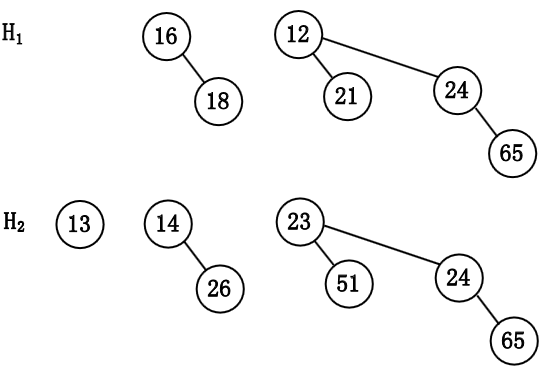
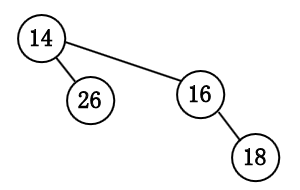
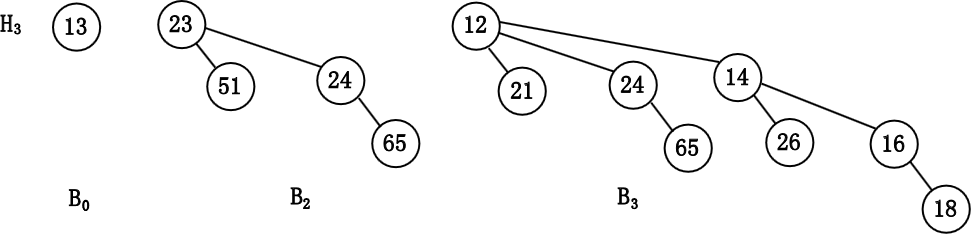
由于几乎使用任意合理的实现方法合并两棵二项树均花费常数时间, 而总共存在
为使该操作更有效, 我们需要将这些树放到按照高度排序的二项队列中.
插入实际上是特殊情形的合并, 只要创建一棵单结点树并执行一次合并即可. 这种操作的最坏情形运行时间也是
更准确地说, 如果元素将要插入的那个优先队列中
我们依次插入 $1$ 到 $7$ 来构成一个二项队列.

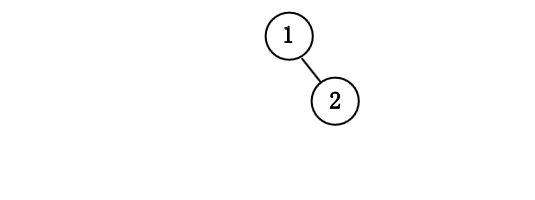
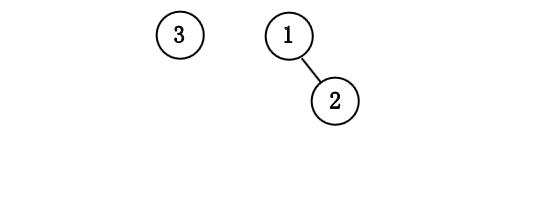
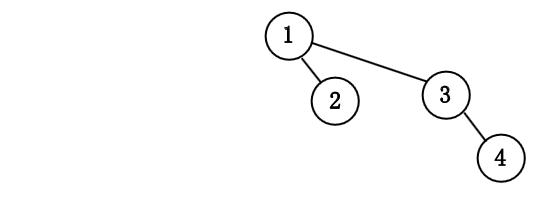
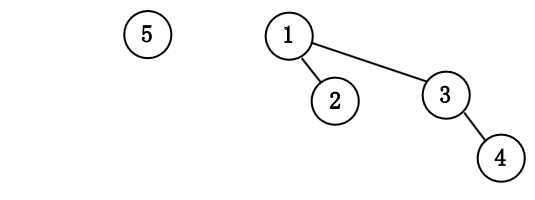
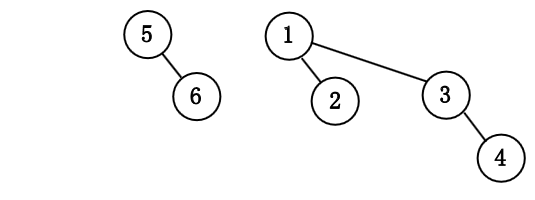
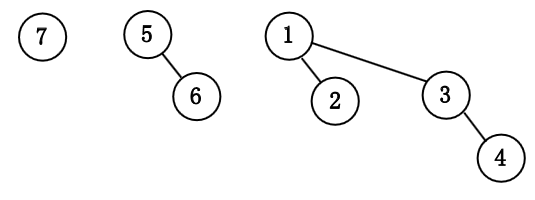
令该树为 $B_k$, 并令原始的优先队列为 $H$.
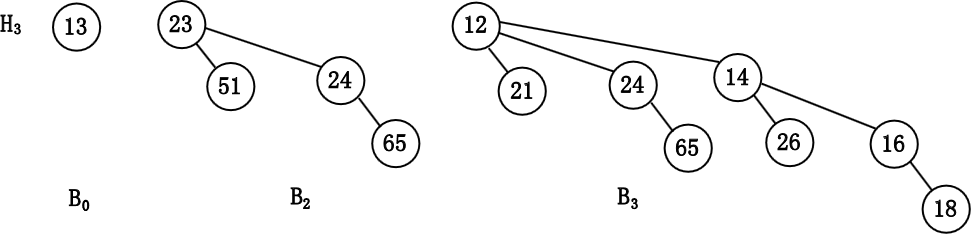
注意 $B_3$ 中含有最小元, 因此删除 $B_3$, 得到新的二项队列 $H'=\{B_0,B_2\}$.
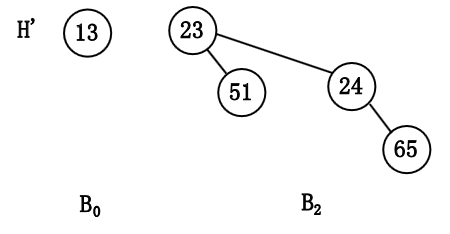
将 $B_3$ 的根删除, 得到二项队列 $H''$.
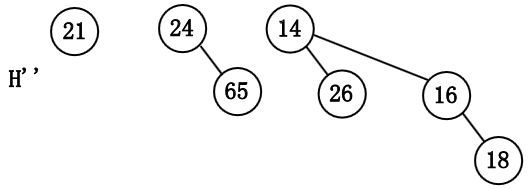
将两个二项队列 $H'$ 和 $H''$ 合并.
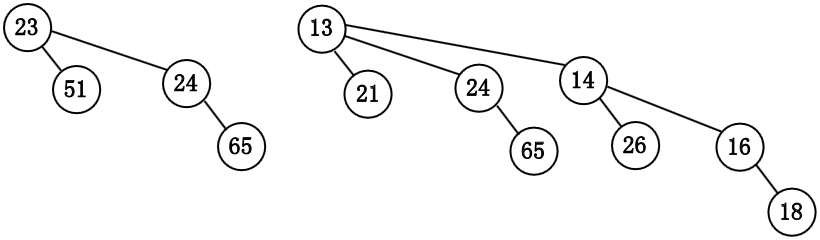
该操作还要求诸儿子按照它们的子树的大小排序.
我们还需要保证很容易合并两棵树. 当两棵树被合并时, 其中一棵树作为儿子加到另一棵树上. 由于这棵新树将是最大的子树, 因此, 以大小递减的方式保持这些子树是有意义的. 只有这时我们才能够有效地合并两棵二项树从而合并两个二项队列. 二项队列是二项树的数组.
总之, 二项树的每一个结点将包含数据、第一个儿子以及右兄弟.
二项树中的儿子以递减次序排列.
template <typename Comparable>
class BinomialQueue
{
public:
BinomialQueue( );
BinomialQueue( const Comparable & item );
BinomialQueue( const BinomialQueue & rhs );
~BinomialQueue( );
bool isEmpty( ) const;
const Comparable & findMin( ) const;
void insert( const Comparable & x );
void deleteMin( );
void deleteMin( Comparable & minItem );
void makeEmpty( );
void merge( BinomialQueue & rhs );
const BinomialQueue & operator= ( const BinomialQueue & rhs );
private:
struct BinomialNode
{
Comparable element;
BinomialNode *leftChild;
BinomialNode *nextSibling;
BinomialNode( const Comparable & theElement,
BinomialNode *lt, BinomialNode *rt )
: element( theElement ), leftChild( lt ), nextSibling( rt ) { }
};
enum { DEFAULT_TREES = 1 };
int currentSize; // Number of items in priority queue
vector<BinomialNode *> theTrees; // An array of tree roots
int findMinIndex( ) const;
int capacity( ) const;
BinomialNode * combineTrees( BinomialNode *t1, BinomialNode *t2 );
void makeEmpty( BinomialNode * & t );
BinomialNode * clone( BinomialNode *t ) const;
};
/**
* Return the result of merging equal-sized t1 and t2.
*/
BinomialNode * combineTrees( BinomialNode *t1, BinomialNode *t2 )
{
if( t2->element < t1->element )
{
return combineTrees( t2, t1 );//在真正执行合并两棵二项树时, 总是令第一个参数 t1 指向的 element 之小于等于第二个参数 t2 所指向的 element 值.
}
//于是按合并的规则, t2 这棵树将接到 t1, 即 t2 指向的结点作为 t1 指向结点的儿子.
//具体的,
t2->nextSibling = t1->leftChild;// t1的leftChild(脱离t1)成为t2的nextSibling.
t1->leftChild = t2;//t2成为t1的leftChild.
return t1;
}
注意这里树结构的存储与往常不同, 每个结点将其最右边的儿子当作第一个儿子, 然后从右向左找 nextSibling.
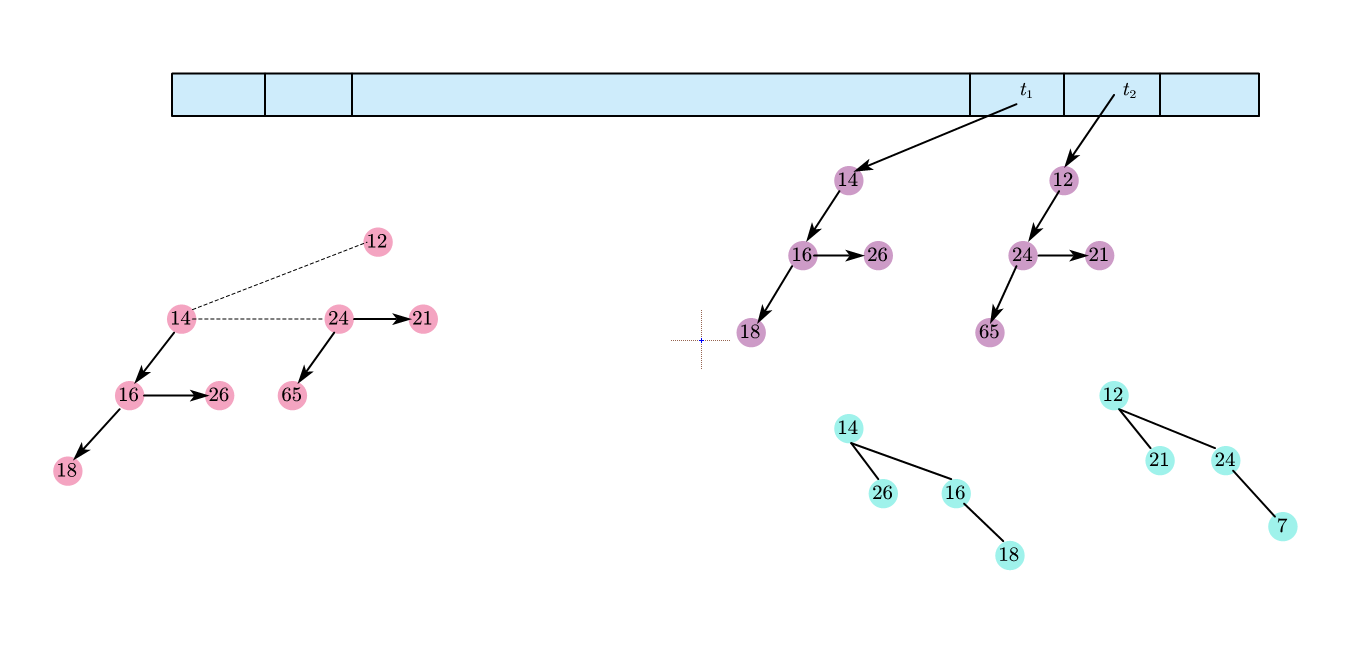
/**
* Merge rhs into the priority queue.
* rhs becomes empty. rhs must be different from this.
*/
void merge( BinomialQueue & rhs )
{
if( this == &rhs ) // Avoid aliasing problems
return;
currentSize += rhs.currentSize;
if( currentSize > capacity( ) )
{
int oldNumTrees = theTrees.size( );
int newNumTrees = max( theTrees.size( ), rhs.theTrees.size( ) ) + 1;
theTrees.resize( newNumTrees );
for( int i = oldNumTrees; i < newNumTrees; i++ )
theTrees[ i ] = NULL;
}
BinomialNode *carry = NULL;
for( int i = 0, j = 1; j <= currentSize; i++, j *= 2 )
{
//思考 j *= 2 的作用是什么?(Exercise)
BinomialNode *t1 = theTrees[ i ];
//判断 i 是否超过了将要合并的二项队列rhs中二项树的个数, 如果是, 则令结点为 NULL.
BinomialNode *t2 = i < rhs.theTrees.size( ) ? rhs.theTrees[ i ]
: NULL;
//事实上, t1 指向当前二项队列中的二项树, t2 指向 rhs 中的二项树.
int whichCase = t1 == NULL ? 0 : 1;
whichCase += t2 == NULL ? 0 : 2;
whichCase += carry == NULL ? 0 : 4;
/*
carry t2 t1
x_1 x_2 x_3
-----------------
where x_i=0 or 1, there are 8 cases.
*/
switch( whichCase )
{
case 0: /* No trees */
case 1: /* Only this */
break;
case 2: /* Only rhs */
theTrees[ i ] = t2;
rhs.theTrees[ i ] = NULL;
break;
case 4: /* Only carry */
theTrees[ i ] = carry;
carry = NULL;
break;
case 3: /* this and rhs */
//carry 是由高度相同的两棵树进行合并而来.
carry = combineTrees( t1, t2 );
theTrees[ i ] = rhs.theTrees[ i ] = NULL;//注意此步清空 this 和 rhs 这两棵树,因为已经合并.
break;
case 5: /* this and carry */
carry = combineTrees( t1, carry );
theTrees[ i ] = NULL;
break;
case 6: /* rhs and carry */
carry = combineTrees( t2, carry );
rhs.theTrees[ i ] = NULL;
break;
case 7: /* All three */
theTrees[ i ] = carry;
carry = combineTrees( t1, t2 );
rhs.theTrees[ i ] = NULL;
break;
}
}
//将 rhs 这个二项队列清空.
for( int k = 0; k < rhs.theTrees.size( ); k++ )
rhs.theTrees[ k ] = NULL;
rhs.currentSize = 0;
}
这里循环中每次执行
/**
* Remove the minimum item and place it in minItem.
* Throws UnderflowException if empty.
*/
void deleteMin( Comparable & minItem )
{
if( isEmpty( ) )
throw UnderflowException( );
int minIndex = findMinIndex( );
minItem = theTrees[ minIndex ]->element;
BinomialNode *oldRoot = theTrees[ minIndex ];
BinomialNode *deletedTree = oldRoot->leftChild;
delete oldRoot;//删除最小元
//找到最小元后, 将这个最小元所在的二项树的根结点删除, 得到新的二项队列 H''
// Construct H''
BinomialQueue deletedQueue;
deletedQueue.theTrees.resize( minIndex + 1 );// 若最小元在 B_k, 则其儿子数为 k 个
deletedQueue.currentSize = ( 1 << minIndex ) - 1;// 若 minIndex=k, 则 (1 << minIndex) 返回 2^k
//构造二项队列, 将 B_k 的各个儿子作为二项树保存到向量(队列)中.
for( int j = minIndex - 1; j >= 0; j-- )
{
deletedQueue.theTrees[ j ] = deletedTree;//先保存第一个左儿子
deletedTree = deletedTree->nextSibling;// 左儿子下一个兄弟作为左儿子的角色
deletedQueue.theTrees[ j ]->nextSibling = NULL;// 割断原左儿子与它下一个兄弟之间的联系.
}
// Construct H'
// 构造 H' 的过程很简单, 即删除最小元所在的二项树 B_k
theTrees[ minIndex ] = NULL;//删除 B_k
currentSize -= deletedQueue.currentSize + 1;// 不要忘了改变 currentSize 的大小.
merge( deletedQueue );// 最后将 H' 和 H'' 合并. this 指向 H', 而 deletedQueue 指向 H''
}
/**
* Find index of tree containing the smallest item in the priority queue.
* The priority queue must not be empty.
* Return the index of tree containing the smallest item.
*/
int findMinIndex( ) const
{
int i;
int minIndex;
// 跳过前面的各个空树.
for( i = 0; theTrees[ i ] == NULL; i++ )
;
for( minIndex = i; i < theTrees.size( ); i++ )
if( theTrees[ i ] != NULL &&
theTrees[ i ]->element < theTrees[ minIndex ]->element )
minIndex = i;
return minIndex;
}
在 STL 中, 二叉堆是通过称为
STL 实现的是最大堆(max-heap)而不是最小堆(min-heap), 于是所访问的项都是最大项而非最小项.
主要成员函数有
void push( const Object & x );// 将 x 添加到优先队列中 const Object & top( ) const; // 返回优先队列中的最大项 void pop( ); // 删除优先队列中的最大项. (由于允许重复, 所以如果有若干最大项, 则只删除其中一个.) bool empty( ); void clear( );
#include <iostream>
#include <vector>
#include <queue>
#include <functional>
#include <string>
using namespace std;
// Empty the priority queue and print its contents.
template <typename PriorityQueue>
void dumpContents( const string & msg, PriorityQueue & pq )
{
cout << msg << ":" << endl;
while( !pq.empty( ) )
{
cout << pq.top( ) << endl;
pq.pop( );
}
}
// Do some inserts and removes (done in dumpContents).
int main( )
{
//默认得到最大堆
priority_queue<int> maxPQ;
//使用 greater 函数对象作为比较器可以得到最小堆.
priority_queue<int,vector<int>,greater<int> > minPQ;
minPQ.push( 4 ); minPQ.push( 3 ); minPQ.push( 5 );
maxPQ.push( 4 ); maxPQ.push( 3 ); maxPQ.push( 5 );
dumpContents( "minPQ", minPQ ); // 3 4 5
dumpContents( "maxPQ", maxPQ ); // 5 4 3
return 0;
}
我们已经看到优先队列的各种实现方法和用途.
标准的二叉堆实现简单、速度快,很雅致. 并且不需要链表, 只需要常量的附加空间, 且有效地支持优先队列的操作.
我们考虑了附加的 merge 操作, 开发了三种实现方法, 每种都有其独到之处.
左式堆是展现递归之功能的完美实例.
斜堆则代表缺少平衡原则的一种重要的数据结构.
二项队列表现出, 一个简单的想法如何用来达到好的时间界.