GAP 的版权
GAP 的版权

Groups, Algorithms, Programming
www.gap-system.org
GAP website: www.gap-system.org
Original Document: http://www-circa.mcs.st-and.ac.uk/gapintro0.php
http://www.math.colostate.edu/~hulpke

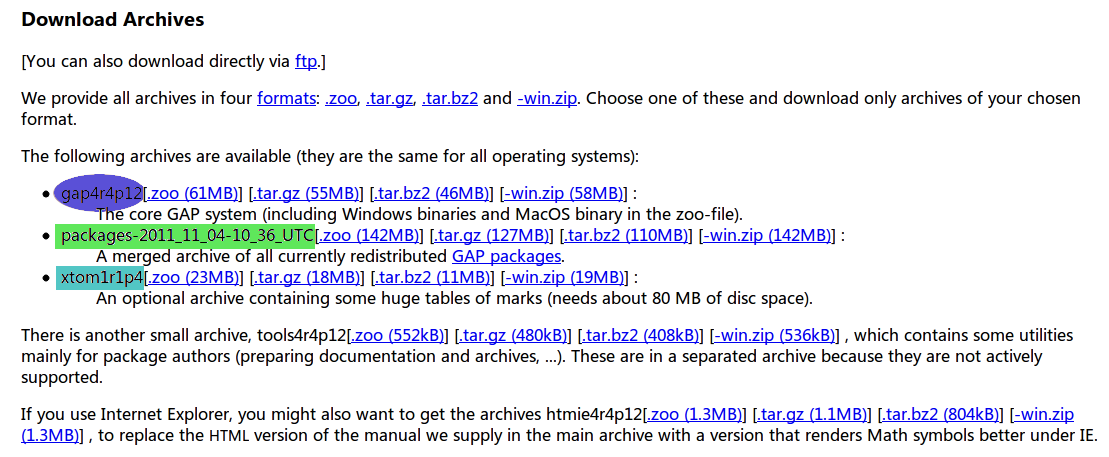

sudo apt-get install gap
./configure
make

.configure ../..
make
if has("syntax")
syntax on " Default to no syntax highlightning
endif
" For GAP files
augroup gap
" Remove all gap autocommands
au!
autocmd BufRead,BufNewFile *.g,*.gi,*.gd source ~/.vim/gap.vim
autocmd BufRead,BufNewFile *.g,*.gi,*.gd set filetype=gap comments=s:##\ \ ,m:##\ \ ,e:##\ \ b:#
" I'm using the external program `par' for formating comment lines starting
" with `## '. Include these lines only when you have par installed.
autocmd BufRead,BufNewFile *.g,*.gi,*.gd set formatprg="par w76p4s0j"
autocmd BufWritePost,FileWritePost *.g,*.gi,*.gd set formatprg="par w76p0s0j"
augroup END

/usr/bin/gap /usr/bin/gap.real /usr/bin/update-gap-workspace /usr/lib/gap/sysinfo.gap /usr/share/doc/gap-core/changelog-3.4.Debian.gz /usr/share/doc/gap-core/changelog-4.2.Debian.gz /usr/share/doc/gap-core/changelog.Debian.gz /usr/share/doc/gap-core/copyright /usr/share/doc/gap-core/description4r4p10.gz /usr/share/doc/gap-core/description4r4p11.gz /usr/share/doc/gap-core/description4r4p12 /usr/share/doc/gap-core/description4r4p5.gz /usr/share/doc/gap-core/description4r4p6.gz /usr/share/doc/gap-core/description4r4p7.gz /usr/share/doc/gap-core/description4r4p8.gz /usr/share/doc/gap-core/description4r4p9 /usr/share/doc/gap-core/etc/README.vim-utils /usr/share/doc/gap-core/etc/gap.vim.gz /usr/share/doc/gap-core/etc/gap_indent.vim /usr/share/gap/sysinfo.gap /usr/share/man/man1/gap.1.gz /usr/share/man/man1/gap.real.1.gz /usr/share/man/man1/update-gap-workspace.1.gz /usr/share/menu/gap-core /usr/share/pixmaps/gap.xpm
(2 + 3)*(7 - 5);
10
2*3/66;
1/11
2^100-1;
1267650600228229401496703205375
5/2 + 3/5;
31/10
66/1512 + 1/252;
1/21
Sqrt(100);
10
Sqrt(100) in Integers;
true
Sqrt(99) in Integers;
false
Let us comment here regarding spaces in the input. We could (and often do) leave spaces round the contents of brackets. For example
Sqrt( 100 );
10
More spaces (although we wouldn't in general suggest that anyone does this) are still OK.
Sqrt( 100 );
10
We can even leave a space before the (.
Sqrt ( 100 );
10
However, we obviously can't leave spaces in the middle of commands or numbers. For example the following will produce an error.
Sqr t(100);
Variable: 'Sqr' must have a value
Syntax error: ; expected
Sqr t(100);
^
100
Sqrt(10 0);
Syntax error: ) expected
Sqrt(10 0);
^
We return to giving commands for the manipulation of numbers.
(66/1512 + 1/252) in Rationals;
true
(66/1512 + 1/252) in Integers;
false
We can find Greatest Common Divisors of integers
Gcd(1512,1215);
27
Gcd(1020,1512,1215);
3
and their Least Common Multiples.
Lcm(1512,1215);
68040
Lcm(1020,1512,1215);
1156680
Given two integers $a$, $b$ with greatest common divisor $d$ we can find $x$, $y$ such that $xa+yb=d$ with Gcdex(a,b):
a:= 1512;; b:= 1215;;
g:= Gcdex(a,b);
rec( gcd := 27, coeff1 := -4, coeff2 := 5, coeff3 := 45, coeff4 := -56 )
Note that "rec" indicates a record with various components.
d:= g.gcd;; x:= g.coeff1;; y:= g.coeff2;;
d= a*x+b*y;
true
Notice the use of ;;
to avoid GAP printing back the input line.
To work mod n we can use the obvious method.
(5 + 7) mod 9;
3
3^7 mod 10;
7
However, to compute large powers mod n it is better to use PowerModInt.
PowerModInt(2, 1000, 10);
6
gives the same result as
2^1000 mod 10;
6
What do you think PowerModInt does and why do you think it might be faster?
So if we want to compute 1000251291 mod 251291 we should use
PowerModInt(1000, 251291, 251291);
1000
Is this the answer you expect? Try
PowerModInt(1001, 251291, 251291);
1001
PowerModInt(1002, 251291, 251291);
1002
PowerModInt(1003, 251291, 251291);
1003
What well known theorem does this illustrate?
What about
PowerModInt(1000, 251293, 251293);
64280
If $p$ is a prime number, then \[ a^p\equiv a\quad(\text{mod}\ p) \]
IsPrime(251291);
true
IsPrime(251293);
false
Another useful function for working with integers is RootsMod
which finds modular roots.
RootsMod(4, 15);
[ 2, 7, 8, 13 ]
finds all the square roots of 4 mod 15. It has the same effect as
RootsMod(4, 2, 15);
[ 2, 7, 8, 13 ]
For the cube roots of 4 mod 15 use
RootsMod(4, 3, 15);
[ 4 ]
In fact the RootsMod
function returns a set. We now look further at sets and lists.
GAP writes its lists with [ ].
We can define a list using a range.
r_1:= [ 1..10 ];
[ 1 .. 10 ]
This list $r_1$ consists of all the integers from 1 to 10. For example:
5 in r_1;
true
11 in r_1;
false
The list $r_1$ contains Length(r_1) or Size(r_1) elements
Length(r_1);
10
GAP will also use ranges to produce an arithmetic progression. For example:
r_2:=[1,3..17];
[ 1, 3 .. 17 ]
We can get GAP to display the elements of the list.
Elements(r_2);
[ 1, 3, 5, 7, 9, 11, 13, 15, 17 ]
More examples:
r_3:=[2,4..16];
[ 2, 4 .. 16 ]
Elements(r_3);
[ 2, 4, 6, 8, 10, 12, 14, 16 ]
r_4:=[5,8..35];
[ 5, 8 .. 35 ]
Elements(r_4);
[ 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35 ]
We can also write out all the elements to define a list:
s:= [ 1, 8, 6, 2 ];
[ 1, 8, 6, 2 ]
GAP will do a form of arithmetic with lists.
We can generate the same arithmetic progression as before:
2*[1..9]-1;
[ 1, 3, 5, 7, 9, 11, 13, 15, 17 ]
We can add or subtract lists -- even of different lengths
[1,2,3]+[4,5];
[ 5, 7, 3 ]
We can add new elements to lists. GAP does not return any output to the screen.
t:=[ 1, 2, 2, 3, 4, 5, 6 ];
[ 1, 2, 2, 3, 4, 5, 6 ]
Add(t, 10);
But we can see what has happened:
t;
[ 1, 2, 2, 3, 4, 5, 6, 10 ]
The command Add
will simply add an entry to the end of an existing list. If we want to create a new list which is equal to the original list but has an added element we can first make a copy of the list and then add the element. For example
lis:= [1,2,1,2,5,9];
[ 1, 2, 1, 2, 5, 9 ]
newlis:= ShallowCopy(lis);
[ 1, 2, 1, 2, 5, 9 ]
GAP has various commands for copying and ShallowCopy is the one we need here. We can now modify our copy without changing the original list.
Add(newlis, -5);
lis; newlis;
[ 1, 2, 1, 2, 5, 9 ]
[ 1, 2, 1, 2, 5, 9, -5 ]
We can filter out elements from a list with particular properties. For example to find all the elements in the list t which are prime we input
t1:= Filtered(t, IsPrimeInt);
[ 2, 2, 3, 5 ]
To filter out the elements which have a given property, one must use Filtered(t, f)
where $f$ is a function which takes the value true on the elements to be filtered. We will discuss functions later.
GAP will sometimes consider a list as a set, but often needs to convert it before applying set operations.
s:= [ 1, 8, 6, 2 ];
[ 1, 8, 6, 2 ]
We test if it is a set:
IsSet(s);
false
GAP will only count a list of integers as a set if it is ordered increasingly and contains no repetitions. The next example has a repeated entry.
t:= [ 1, 2, 2, 3, 4, 5, 6 ];
[ 1, 2, 2, 3, 4, 5, 6 ]
IsSet(t);
false
Of course s and t are lists and we can create sets from them:
ss:= Set(s);
[ 1, 2, 6, 8 ]
tt:= Set(t);
[ 1, 2, 3, 4, 5, 6 ]
Notice that this operation removes repetitions and puts the elements into increasing order.
The usual set operations work and GAP treats the lists as if they were sets before applying the operations:
Intersection(s, t);
[ 1, 2, 6 ]
IsEqualSet(Intersection(s,t),Intersection
(ss,tt));
true
Union(s, t);
[ 1, 2, 3, 4, 5, 6, 8 ]
Difference(s, t);
[ 8 ]
Difference(t, s);
[ 3, 4, 5 ]
To add an element to the set ss we use AddSet. Again we get no output.
AddSet(ss, 4);
ss;
[ 1, 2, 4, 6, 8 ]
We begin with elementary loops.
for i in [1..10] do
Print(i);
od;
12345678910
Notice that the output is 12345678910. Suppose we want to print a space between consecutive numbers.
for i in [1..10] do
Print(i," ");
od;
1 2 3 4 5 6 7 8 9 10
Suppose we want to print each number on a separate line. We use "\n" to make a new line.
for i in [1..10] do
Print(i, "\n");
od;
1
2
3
4
5
6
7
8
9
10
A slightly more useful loop might be:
for i in [1..10] do
Print(i," squared is ",i^2,"\n");
od;
1 squared is 1
2 squared is 4
3 squared is 9
4 squared is 16
5 squared is 25
6 squared is 36
7 squared is 49
8 squared is 64
9 squared is 81
10 squared is 100
Notice that we have put spaces in " squared is " so that it displays properly.
We now introduce conditionals into our loop. We test to see if an integer i is prime and if so we print it.
for i in [1..20] do
if IsPrimeInt(i) then Print(i, " is prime ", "\n"); fi;
od;
2 is prime
3 is prime
5 is prime
7 is prime
11 is prime
13 is prime
17 is prime
19 is prime
Of course most even numbers cannot be prime so we could reduce the number of times the loop is run by only looking at odd numbers. However, 2 will not be listed!
for i in [1, 3 .. 19] do
if IsPrimeInt(i) then
Print(i," is prime ","\n");
fi;
od;
3 is prime
5 is prime
7 is prime
11 is prime
13 is prime
17 is prime
19 is prime
The next loop prints the primes in the first 50 terms of the Fibonacci sequence.
for i in [1..50] do
if IsPrimeInt(Fibonacci(i)) then
Print(Fibonacci(i)," is prime ","\n");
fi;
od;
2 is prime
3 is prime
5 is prime
13 is prime
89 is prime
233 is prime
1597 is prime
28657 is prime
514229 is prime
433494437 is prime
2971215073 is prime
We can test whether numbers less than 1000 are primes in another way, rather than use IsPrimeInt. For example
13 in Primes;
true
Fibonacci(13) in Primes;
true
Note however that Primes only contains the 168 primes less than 1000. For example
IsPrimeInt(1597);
true
1597 in Primes;
false
We move on to functions. The following code defines a function that simply squares the argument it is given.
squared:= function(n);
return n^2;
end;
function( n ) ... end
If you want to see the function written out fully, you can ask GAP to Print it.
Print(squared);
function ( n )
;
return n ^ 2;
end
Try applying this function and see the result.
squared(12345);
152399025
There are simpler ways to write easy functions like this. For example
cubed:= n -> n^3;
function( n ) ... end
Print(cubed);
function ( n )
return n ^ 3;
end
cubed(123456);
1881640295202816
We can produce lists of cubes as follows:
List( [1..10], cubed );
[ 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000 ]
This is a very useful construction. Here are a few more examples.
First the squares of the even numbers between 2 and 14.
List( [2,4..14], n->n^2 );
[ 4, 16, 36, 64, 100, 144, 196 ]
A more complicated example
f:=function(n);
if n mod 2 =0 then
return n^2;
else
return n^3;
fi;
end;
function( n ) ... end
List( [1..20], f);
[ 1, 4, 27, 16, 125, 36, 343, 64, 729, 100, 1331, 144, 2197, 196, 3375, 256, 4913, 324, 6859, 400 ]
If we define a function which returns true or false, we may use this to filter a list.
is1mod4:=function(n);
if n mod 4 = 1 then
return true;
else
return false;
fi;
end;
function( n ) ... end
Filtered([1..20], is1mod4);
[ 1, 5, 9, 13, 17 ]
There is a famous open question which asks whether one always reaches 1 if one starts with any number and successively applies that rule. For example, if we start with 3 we get
3, 10, 5, 16, 8, 4, 2, 1
f:= function(n);
if n mod 2 = 0 then
return n/2;
else
return 3*n+1;
fi;
end;
function( n ) ... end
Let us now write a function t to return the number of steps that are required to reach 1. Note that we define local variables to use in the function. We do this so that if variables with the same name are used elsewhere their value will not be affected by the function. Note that there is no semi-colon before the local variables are listed.
t:= function(i) local k, m;
k:= 0;
m:= i;
while m > 1 do
k:= k+1;
m:= f(m);
od;
return k;
end;
function( i ) ... end
When we wrote the code for the function we put extra spaces at the beginning of each line so that it was easier to see where conditional clauses and loops began and ended.
Let us produce a sequence with ith entry the number of steps required to reach 1 starting from i.
s:= List( [1..1000], t );
[ 0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, 7, 15, 15, 10, 23, 10, 111, 18, 18, 18, 106, 5, 26, 13, 13, 21, 21, 21, 34, 8, 109, 8, 29, 16, 16, 16, 104, 11, 24, 24, 24, 11, 11, 112, 112, 19, 32, 19, 32, 19, 19, 107, 107, 6, 27, 27, 27, 14, 14, 14, 102, 22, 115, 22, 14, 22, 22, 35, 35, 9, 22, 110, 110, 9, 9, 30, 30, 17, 30, 17, 92, 17, 17, 105, 105, 12, 118, 25, 25, 25, 25, 25, 87, 12, 38, 12, 100, 113, 113, 113, 69, 20, 12, 33, 33, 20, 20, 33, 33, 20, 95, 20, 46, 108, 108, 108, 46, 7, 121, 28, 28, 28, 28, 28, 41, 15, 90, 15, 41, 15, 15, 103, 103, 23, 116, 116, 116, 23, 23, 15, 15, 23, 36, 23, 85, 36, 36, 36, 54, 10, 98, 23, 23, 111, 111, 111, 67, 10, 49, 10, 124, 31, 31, 31, 80, 18, 31, 31, 31, 18, 18, 93, 93, 18, 44, 18, 44, 106, 106, 106, 44, 13, 119, 119, 119, 26, 26, 26, 119, 26, 18, 26, 39, 26, 26, 88, 88, 13, 39, 39, 39, 13, 13, 101, 101, 114, 26, 114, 52, 114, 114, 70, 70, 21, 52, 13, 13, 34, 34, 34, 127, 21, 83, 21, 127, 34, 34, 34, 52, 21, 21, 96, 96, 21, 21, 47, 47, 109, 47, 109, 65, 109, 109, 47, 47, 8, 122, 122, 122, 29, 29, 29, 78, 29, 122, 29, 21, 29, 29, 42, 42, 16, 29, 91, 91, 16, 16, 42, 42, 16, 42, 16, 60, 104, 104, 104, 42, 24, 29, 117, 117, 117, 117, 117, 55, 24, 73, 24, 117, 16, 16, 16, 42, 24, 37, 37, 37, 24, 24, 86, 86, 37, 130, 37, 37, 37, 37, 55, 55, 11, 24, 99, 99, 24, 24, 24, 143, 112, 50, 112, 24, 112, 112, 68, 68, 11, 112, 50, 50, 11, 11, 125, 125, 32, 125, 32, 125, 32, 32, 81, 81, 19, 125, 32, 32, 32, 32, 32, 50, 19, 45, 19, 45, 94, 94, 94, 45, 19, 19, 45, 45, 19, 19, 45, 45, 107, 63, 107, 58, 107, 107, 45, 45, 14, 32, 120, 120, 120, 120, 120, 120, 27, 58, 27, 76, 27, 27, 120, 120, 27, 19, 19, 19, 27, 27, 40, 40, 27, 40, 27, 133, 89, 89, 89, 133, 14, 133, 40, 40, 40, 40, 40, 32, 14, 58, 14, 53, 102, 102, 102, 40, 115, 27, 27, 27, 115, 115, 53, 53, 115, 27, 115, 53, 71, 71, 71, 97, 22, 115, 53, 53, 14, 14, 14, 40, 35, 128, 35, 128, 35, 35, 128, 128, 22, 35, 84, 84, 22, 22, 128, 128, 35, 35, 35, 27, 35, 35, 53, 53, 22, 48, 22, 22, 97, 97, 97, 141, 22, 48, 22, 141, 48, 48, 48, 97, 110, 22, 48, 48, 110, 110, 66, 66, 110, 61, 110, 35, 48, 48, 48, 61, 9, 35, 123, 123, 123, 123, 123, 61, 30, 123, 30, 123, 30, 30, 79, 79, 30, 30, 123, 123, 30, 30, 22, 22, 30, 22, 30, 48, 43, 43, 43, 136, 17, 43, 30, 30, 92, 92, 92, 43, 17, 136, 17, 30, 43, 43, 43, 87, 17, 43, 43, 43, 17, 17, 61, 61, 105, 56, 105, 30, 105, 105, 43, 43, 25, 30, 30, 30, 118, 118, 118, 30, 118, 56, 118, 118, 118, 118, 56, 56, 25, 74, 74, 74, 25, 25, 118, 118, 17, 56, 17, 69, 17, 17, 43, 43, 25, 131, 38, 38, 38, 38, 38, 69, 25, 131, 25, 131, 87, 87, 87, 131, 38, 25, 131, 131, 38, 38, 38, 38, 38, 30, 38, 30, 56, 56, 56, 131, 12, 51, 25, 25, 100, 100, 100, 38, 25, 144, 25, 100, 25, 25, 144, 144, 113, 51, 51, 51, 113, 113, 25, 25, 113, 51, 113, 144, 69, 69, 69, 95, 12, 64, 113, 113, 51, 51, 51, 64, 12, 64, 12, 38, 126, 126, 126, 38, 33, 126, 126, 126, 33, 33, 126, 126, 33, 126, 33, 64, 82, 82, 82, 170, 20, 33, 126, 126, 33, 33, 33, 64, 33, 25, 33, 25, 33, 33, 51, 51, 20, 46, 46, 46, 20, 20, 46, 46, 95, 33, 95, 139, 95, 95, 46, 46, 20, 139, 20, 20, 46, 46, 46, 95, 20, 90, 20, 46, 46, 46, 46, 139, 108, 20, 64, 64, 108, 108, 59, 59, 108, 33, 108, 152, 46, 46, 46, 59, 15, 33, 33, 33, 121, 121, 121, 152, 121, 33, 121, 59, 121, 121, 121, 121, 28, 121, 59, 59, 28, 28, 77, 77, 28, 77, 28, 103, 121, 121, 121, 72, 28, 59, 20, 20, 20, 20, 20, 72, 28, 46, 28, 134, 41, 41, 41, 134, 28, 41, 41, 41, 28, 28, 134, 134, 90, 134, 90, 41, 90, 90, 134, 134, 15, 28, 134, 134, 41, 41, 41, 85, 41, 41, 41, 41, 41, 41, 33, 33, 15, 59, 59, 59, 15, 15, 54, 54, 103, 28, 103, 147, 103, 103, 41, 41, 116, 147, 28, 28, 28, 28, 28, 178, 116, 147, 116, 28, 54, 54, 54, 147, 116, 116, 28, 28, 116, 116, 54, 54, 72, 147, 72, 46, 72, 72, 98, 98, 23, 67, 116, 116, 54, 54, 54, 116, 15, 67, 15, 54, 15, 15, 41, 41, 36, 129, 129, 129, 36, 36, 129, 129, 36, 129, 36, 67, 129, 129, 129, 116, 23, 129, 36, 36, 85, 85, 85, 129, 23, 173, 23, 85, 129, 129, 129, 36, 36, 36, 36, 36, 36, 36, 28, 28, 36, 28, 36, 28, 54, 54, 54, 129, 23, 49, 49, 49, 23, 23, 23, 142, 98, 49, 98, 36, 98, 98, 142, 142, 23, 98, 49, 49, 23, 23, 142, 142, 49, 23, 49, 36, 49, 49, 98, 98, 111, 93, 23, 23, 49, 49, 49, 49, 111 ]
If you don't want to see the list s then end the line with ;;
The following loop will product the same list s as we just constructed above but of course takes longer to write.
s:= [];; for i in [1..1000] do Add(s, t(i)); od; Print(s, "\n");
[ 0, 1, 7, 2, 5, 8, 16, 3, 19, 6, 14, 9, 9, 17, 17, 4, 12, 20, 20, 7, 7, 15, 15, 10, 23, 10, 111, 18, 18, 18, 106, 5, 26, 13, 13, 21, 21, 21, 34, 8, 109, 8, 29, 16, 16, 16, 104, 11, 24, 24, 24, 11, 11, 112, 112, 19, 32, 19, 32, 19, 19, 107, 107, 6, 27, 27, 27, 14, 14, 14, 102, 22, 115, 22, 14, 22, 22, 35, 35, 9, 22, 110, 110, 9, 9, 30, 30, 17, 30, 17, 92, 17, 17, 105, 105, 12, 118, 25, 25, 25, 25, 25, 87, 12, 38, 12, 100, 113, 113, 113, 69, 20, 12, 33, 33, 20, 20, 33, 33, 20, 95, 20, 46, 108, 108, 108, 46, 7, 121, 28, 28, 28, 28, 28, 41, 15, 90, 15, 41, 15, 15, 103, 103, 23, 116, 116, 116, 23, 23, 15, 15, 23, 36, 23, 85, 36, 36, 36, 54, 10, 98, 23, 23, 111, 111, 111, 67, 10, 49, 10, 124, 31, 31, 31, 80, 18, 31, 31, 31, 18, 18, 93, 93, 18, 44, 18, 44, 106, 106, 106, 44, 13, 119, 119, 119, 26, 26, 26, 119, 26, 18, 26, 39, 26, 26, 88, 88, 13, 39, 39, 39, 13, 13, 101, 101, 114, 26, 114, 52, 114, 114, 70, 70, 21, 52, 13, 13, 34, 34, 34, 127, 21, 83, 21, 127, 34, 34, 34, 52, 21, 21, 96, 96, 21, 21, 47, 47, 109, 47, 109, 65, 109, 109, 47, 47, 8, 122, 122, 122, 29, 29, 29, 78, 29, 122, 29, 21, 29, 29, 42, 42, 16, 29, 91, 91, 16, 16, 42, 42, 16, 42, 16, 60, 104, 104, 104, 42, 24, 29, 117, 117, 117, 117, 117, 55, 24, 73, 24, 117, 16, 16, 16, 42, 24, 37, 37, 37, 24, 24, 86, 86, 37, 130, 37, 37, 37, 37, 55, 55, 11, 24, 99, 99, 24, 24, 24, 143, 112, 50, 112, 24, 112, 112, 68, 68, 11, 112, 50, 50, 11, 11, 125, 125, 32, 125, 32, 125, 32, 32, 81, 81, 19, 125, 32, 32, 32, 32, 32, 50, 19, 45, 19, 45, 94, 94, 94, 45, 19, 19, 45, 45, 19, 19, 45, 45, 107, 63, 107, 58, 107, 107, 45, 45, 14, 32, 120, 120, 120, 120, 120, 120, 27, 58, 27, 76, 27, 27, 120, 120, 27, 19, 19, 19, 27, 27, 40, 40, 27, 40, 27, 133, 89, 89, 89, 133, 14, 133, 40, 40, 40, 40, 40, 32, 14, 58, 14, 53, 102, 102, 102, 40, 115, 27, 27, 27, 115, 115, 53, 53, 115, 27, 115, 53, 71, 71, 71, 97, 22, 115, 53, 53, 14, 14, 14, 40, 35, 128, 35, 128, 35, 35, 128, 128, 22, 35, 84, 84, 22, 22, 128, 128, 35, 35, 35, 27, 35, 35, 53, 53, 22, 48, 22, 22, 97, 97, 97, 141, 22, 48, 22, 141, 48, 48, 48, 97, 110, 22, 48, 48, 110, 110, 66, 66, 110, 61, 110, 35, 48, 48, 48, 61, 9, 35, 123, 123, 123, 123, 123, 61, 30, 123, 30, 123, 30, 30, 79, 79, 30, 30, 123, 123, 30, 30, 22, 22, 30, 22, 30, 48, 43, 43, 43, 136, 17, 43, 30, 30, 92, 92, 92, 43, 17, 136, 17, 30, 43, 43, 43, 87, 17, 43, 43, 43, 17, 17, 61, 61, 105, 56, 105, 30, 105, 105, 43, 43, 25, 30, 30, 30, 118, 118, 118, 30, 118, 56, 118, 118, 118, 118, 56, 56, 25, 74, 74, 74, 25, 25, 118, 118, 17, 56, 17, 69, 17, 17, 43, 43, 25, 131, 38, 38, 38, 38, 38, 69, 25, 131, 25, 131, 87, 87, 87, 131, 38, 25, 131, 131, 38, 38, 38, 38, 38, 30, 38, 30, 56, 56, 56, 131, 12, 51, 25, 25, 100, 100, 100, 38, 25, 144, 25, 100, 25, 25, 144, 144, 113, 51, 51, 51, 113, 113, 25, 25, 113, 51, 113, 144, 69, 69, 69, 95, 12, 64, 113, 113, 51, 51, 51, 64, 12, 64, 12, 38, 126, 126, 126, 38, 33, 126, 126, 126, 33, 33, 126, 126, 33, 126, 33, 64, 82, 82, 82, 170, 20, 33, 126, 126, 33, 33, 33, 64, 33, 25, 33, 25, 33, 33, 51, 51, 20, 46, 46, 46, 20, 20, 46, 46, 95, 33, 95, 139, 95, 95, 46, 46, 20, 139, 20, 20, 46, 46, 46, 95, 20, 90, 20, 46, 46, 46, 46, 139, 108, 20, 64, 64, 108, 108, 59, 59, 108, 33, 108, 152, 46, 46, 46, 59, 15, 33, 33, 33, 121, 121, 121, 152, 121, 33, 121, 59, 121, 121, 121, 121, 28, 121, 59, 59, 28, 28, 77, 77, 28, 77, 28, 103, 121, 121, 121, 72, 28, 59, 20, 20, 20, 20, 20, 72, 28, 46, 28, 134, 41, 41, 41, 134, 28, 41, 41, 41, 28, 28, 134, 134, 90, 134, 90, 41, 90, 90, 134, 134, 15, 28, 134, 134, 41, 41, 41, 85, 41, 41, 41, 41, 41, 41, 33, 33, 15, 59, 59, 59, 15, 15, 54, 54, 103, 28, 103, 147, 103, 103, 41, 41, 116, 147, 28, 28, 28, 28, 28, 178, 116, 147, 116, 28, 54, 54, 54, 147, 116, 116, 28, 28, 116, 116, 54, 54, 72, 147, 72, 46, 72, 72, 98, 98, 23, 67, 116, 116, 54, 54, 54, 116, 15, 67, 15, 54, 15, 15, 41, 41, 36, 129, 129, 129, 36, 36, 129, 129, 36, 129, 36, 67, 129, 129, 129, 116, 23, 129, 36, 36, 85, 85, 85, 129, 23, 173, 23, 85, 129, 129, 129, 36, 36, 36, 36, 36, 36, 36, 28, 28, 36, 28, 36, 28, 54, 54, 54, 129, 23, 49, 49, 49, 23, 23, 23, 142, 98, 49, 98, 36, 98, 98, 142, 142, 23, 98, 49, 49, 23, 23, 142, 142, 49, 23, 49, 36, 49, 49, 98, 98, 111, 93, 23, 23, 49, 49, 49, 49, 111 ]
Notice the fact that lots of adjacent entries in s are equal. So often beginning with consecutive numbers we find that the same number of steps is required to reach 1. As we reach larger numbers we see three consecutive numbers with this property etc.
We construct a list len whose nth entry will be the number of times n consecutive numbers take the same number of steps. Note that when we reach the end of the list, we do not know whether the next entry would have been the same as the last one and so we do not count this run.
len:= ListWithIdenticalEntries(20, 0);
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
count:= 1;;
for i in [ 2 .. Length(s) ] do
if s[i] = s[i-1] then
count:= count + 1;
else
len[count]:= len[count] + 1;
count:= 1;
fi;
od;
len;
[ 394, 150, 72, 5, 10, 2, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
Remove the trailing 0's in len
i:= Length(len); while len[i] = 0 do Unbind(len[i]); i:= i-1; od; len;
[ 394, 150, 72, 5, 10, 2, 1 ]
For each i print the number of i consecutive integers taking the same number of steps to reach 1.
for i in [1..Length(len)] do
Print("There are ",len[i],
" runs of length ", i, "\n");
od;
There are 394 runs of length 1
There are 150 runs of length 2
There are 72 runs of length 3
There are 5 runs of length 4
There are 10 runs of length 5
There are 2 runs of length 6
There are 1 runs of length 7
We again note that we added spaces in the strings in the Print statement.
Another thing that one can investigate about this problem is the highest number reached by the sequence before it collapses to 1.
We now investigate Stirling numbers of the second kind.
Stirling2(n, r) is the number of ways a set of n elements can be partitioned into r disjoint non-empty subsets.
For example, if $n=2k$, and $r=2$, then \[ \text{Stirling}2(n,2)=\sum_{i=1}^{k-1}C_n^i+\frac{C_n^k}{2}, \]
If $n=2k+1$, then \[ \text{Stirling}2(n,2)=\sum_{i=1}^{k}C_n^i. \]
First we list the these numbers for a fixed n, take n = 12.
l:= List( [1..12], k -> Stirling2(12, k) );
[ 1, 2047, 86526, 611501, 1379400, 1323652, 627396, 159027, 22275, 1705, 66, 1 ]
Find the maximum value
m:= Maximum(l);
1379400
and its position in the list
Position(l, m);
5
Let us now construct a list stir from these lists of Stirling numbers so that the nth entry of stir is the list of Stirling numbers for a set of n elements. This would give a seriously large output, so we suppress it.
stir:= List( [1..50], n -> List([1..n], k -> Stirling2(n, k)) );;
Now find where the maximum occurs for each n.
for i in [1..Length(stir)] do
Print("row ", i, " has maximum in position ",
Position(stir[i], Maximum(stir[i])), "\n");
od;
row 1 has maximum in position 1
row 2 has maximum in position 1
row 3 has maximum in position 2
row 4 has maximum in position 2
row 5 has maximum in position 3
row 6 has maximum in position 3
row 7 has maximum in position 4
row 8 has maximum in position 4
row 9 has maximum in position 4
row 10 has maximum in position 5
row 11 has maximum in position 5
row 12 has maximum in position 5
row 13 has maximum in position 6
row 14 has maximum in position 6
row 15 has maximum in position 6
row 16 has maximum in position 7
row 17 has maximum in position 7
row 18 has maximum in position 7
row 19 has maximum in position 8
row 20 has maximum in position 8
row 21 has maximum in position 8
row 22 has maximum in position 9
row 23 has maximum in position 9
row 24 has maximum in position 9
row 25 has maximum in position 10
row 26 has maximum in position 10
row 27 has maximum in position 10
row 28 has maximum in position 10
row 29 has maximum in position 11
row 30 has maximum in position 11
row 31 has maximum in position 11
row 32 has maximum in position 12
row 33 has maximum in position 12
row 34 has maximum in position 12
row 35 has maximum in position 12
row 36 has maximum in position 13
row 37 has maximum in position 13
row 38 has maximum in position 13
row 39 has maximum in position 14
row 40 has maximum in position 14
row 41 has maximum in position 14
row 42 has maximum in position 14
row 43 has maximum in position 15
row 44 has maximum in position 15
row 45 has maximum in position 15
row 46 has maximum in position 15
row 47 has maximum in position 16
row 48 has maximum in position 16
row 49 has maximum in position 16
row 50 has maximum in position 16
It is not easy to predict where the maximum will occur for a given $n$. However, there is an asymptotic result known, namely that as $n\rightarrow\infty$, the maximum position tends to $n/\ln n$.
We now examine a problem which involves elementary number theory.
Are there infinitely many pairs of consecutive integers with the same number of divisors?
Is there an infinite number of pairs of consecutive integers that each have 4 divisors?
We have no hope of solving the problem but let us investigate it.
First note that DivisorsInt(n) returns a list of divisors of n.
DivisorsInt(1512);
[ 1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 18, 21, 24, 27, 28, 36, 42, 54, 56, 63, 72, 84, 108, 126, 168, 189, 216, 252, 378, 504, 756, 1512 ]
It is easy to find the number of divisors of n.
Length(DivisorsInt(1512));
32
For ease of typing let us define f(n) to be the number of divisors of n.
f:= n -> Length(DivisorsInt(n));
function( n ) ... end
Let us look for pairs of consecutive integers with the same number of divisors.
for i in [1..200] do
if f(i) = f(i+1) then
Print("pair ", i," ", i+1, " has ",f(i), " divisors ", "\n");
fi;
od;
pair 2 3 has 2 divisors
pair 14 15 has 4 divisors
pair 21 22 has 4 divisors
pair 26 27 has 4 divisors
pair 33 34 has 4 divisors
pair 34 35 has 4 divisors
pair 38 39 has 4 divisors
pair 44 45 has 6 divisors
pair 57 58 has 4 divisors
pair 75 76 has 6 divisors
pair 85 86 has 4 divisors
pair 86 87 has 4 divisors
pair 93 94 has 4 divisors
pair 94 95 has 4 divisors
pair 98 99 has 6 divisors
pair 104 105 has 8 divisors
pair 116 117 has 6 divisors
pair 118 119 has 4 divisors
pair 122 123 has 4 divisors
pair 133 134 has 4 divisors
pair 135 136 has 8 divisors
pair 141 142 has 4 divisors
pair 142 143 has 4 divisors
pair 145 146 has 4 divisors
pair 147 148 has 6 divisors
pair 158 159 has 4 divisors
pair 171 172 has 6 divisors
pair 177 178 has 4 divisors
pair 189 190 has 8 divisors
We can easily move to finding three consecutive integers with the same number of divisors.
for i in [1..200] do
if f(i) = f(i+1) and f(i+1)=f(i+2) then
Print("triple ", i," ", i+1, " ", i+2," has ", f(i)," divisors ", "\n");
fi;
od;
triple 33 34 35 has 4 divisors
triple 85 86 87 has 4 divisors
triple 93 94 95 has 4 divisors
triple 141 142 143 has 4 divisors
Then we can look for even longer runs. This code uses a different kind of loop.
i:=1;;
over:=false;;
while not over do
if f(i) = f(i+1) and f(i+1)=f(i+2) and f(i+2)=f(i+3) and f(i+3)=f(i+4) and f(i+4)=f(i+5) and f(i+5)=f(i+6) then
Print("Sequence of length 7 starting ",i," has ",f(i)," divisors \n");
over:=true;
fi;
i:=i+1;
od;
Sequence of length 7 starting 171893 has 8 divisors
As an exercise you may care to turn the above into a function with a parameter n which returns sequences of length n of integers with the same number of divisors.
Can one find such runs of arbitrary length? GAP can help, but won't tell you the answer!
How to improve GAP(编写自己的宏包, 编写GUI)