问题

这个反常积分 $\displaystyle\int_0^{\infty}\frac{1-\cos x}{x^2}\mathrm{d}x$ 是复分析中的一个经典例子. 

思路是考虑复函数 $f(z)=\dfrac{1-e^{iz}}{z^2}$, 这里 $z\in\mathbb{C}$. $z=0$ 是复函数 $f(z)$ 的二重极点. 在构造环路（围道）积分时, 需避开此极点（一般用半径极小的圆周的一段来避开, 这样是为了好计算）, 同时需要将原积分跟此环路中的某一段积分联系在一起, 且其余段的积分也相对容易计算才行.

[思考] 为何不考虑 $f(z)=\dfrac{1-\cos z}{z^2}$ ?

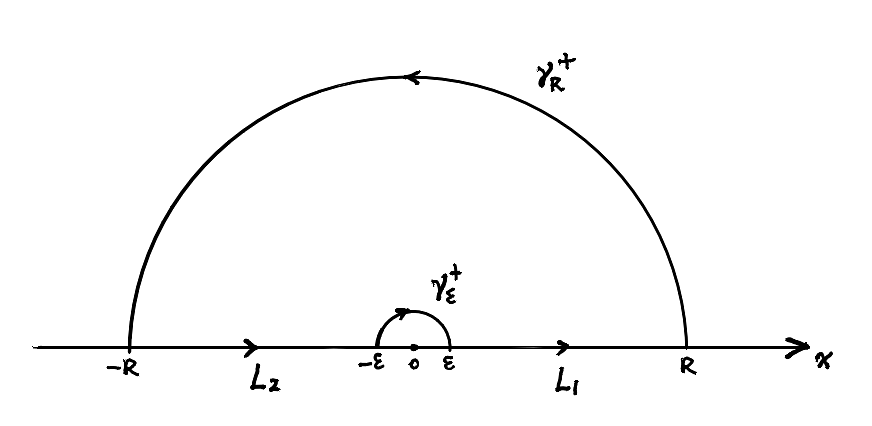
若记 $B_{\varepsilon}(0)$ 为以原点为中心半径为 $\varepsilon$ 的开圆盘, 则取 $\gamma_{\varepsilon}^+$ 为 $B_{\varepsilon}(0)$ 上半部分边界, 方向为从 $(-\varepsilon,0)$ 到 $(\varepsilon,0)$. $L_1$ 为从 $(\varepsilon,0)$ 到 $(R,0)$ 的有向线段,  $\gamma_{R}^+$ 为 $B_{R}(0)$ 上半部分边界, 方向为从 $(R,0)$ 到 $(-R,0)$. $L_2$ 为从 $(-R,0)$ 到 $(-\varepsilon,0)$ 的有向线段. 这四段曲线首尾相接, 构成一个闭回路, 记为 $\Gamma_{\varepsilon}$. 即

\[\Gamma_{\varepsilon}=\gamma_{\varepsilon}^{+} + L_1+\gamma_{R}^{+}+L_2.\]

这里路径上的 $+$ 号指取的是正向. $\Gamma_{\varepsilon}$ 所围的闭区域记为 $\Omega_{\varepsilon}$, 则函数 $\dfrac{1-\cos z}{z^2}$ 在 $\Omega_{\varepsilon}$ 上是解析的. 于是

\[
\int_{\Gamma_{\varepsilon}}\frac{1-e^{iz}}{z^2}\mathrm{d}z=0.
\]

这推出

\[
\int_{L_1}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{\gamma_{R}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{L_2}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{\gamma_{\varepsilon}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z=0.\tag{*}
\]

由于在 $\gamma_{R}^{+}$ 上, $\biggl|\frac{1-e^{iz}}{z^2}\biggr|=\frac{|1-e^{iz}|}{R^2}\leqslant\frac{2}{R^2}$, 因此

\[
\biggl|\int_{\gamma_{R}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z\biggr|=\left|\int_{\gamma_R}\frac{1-e^{iz}}{z^2}\cdot\vec{\tau}\mathrm{d}s\right|\leqslant\int_{\gamma_{R}}\biggl|\frac{1-e^{iz}}{z^2}\biggr|\mathrm{d}s\leqslant\frac{2}{R^2}\cdot\pi R\rightarrow 0,\quad\text{当}\ R\rightarrow\infty.
\]

这里 $\gamma_{R}$ 就是指中心在原点、半径为 $R$ 的(无方向的)上半圆周, $\vec{\tau}$ 是曲线 $\gamma_{R}$ 上的单位切向量. 这里用到了第二类型曲线积分和第一类型曲线积分之间的关系.

\[
e^{iz}=1+\frac{iz}{1!}+\frac{(iz)^2}{2!}+\frac{(iz)^3}{3!}+\cdots
\]

故

\[
\begin{split}
\frac{1-e^{iz}}{z^2}&=-\frac{iz}{z^2}-\frac{1}{z^2}(\frac{(iz)^2}{2!}+\frac{(iz)^3}{3!}+\cdots)\\
&=-\frac{i}{z}+(\frac{1}{2!}+\frac{iz}{3!}-\frac{z^2}{4!}-\frac{iz^3}{5!}+\cdots)\\
&=-\frac{i}{z}+E(z),
\end{split}
\]

这里 $E(z)=\frac{1}{2!}+\frac{iz}{3!}-\frac{z^2}{4!}-\frac{iz^3}{5!}+\cdots$ 当 $z\rightarrow 0$ 是有界的. 故

\[
\int_{\gamma_{\varepsilon}^{+}}E(z)\mathrm{d}z\rightarrow 0,\quad\text{当}\ \varepsilon\rightarrow 0.
\]

而

\[
\int_{\gamma_{\varepsilon}^{+}}\frac{-i}{z}\mathrm{d}z=\int_{\pi}^{0}\frac{-i}{\varepsilon e^{i\theta}}\cdot ie^{i\theta}\mathrm{d}\theta=\int_{\pi}^{0}(-i^2)\mathrm{d}\theta=-\pi.
\]

故

\[
\int_{\gamma_{\varepsilon}^{+}}\frac{1-e^{iz}}{z^2}\mathrm{d}z=\int_{\gamma_{\varepsilon}^{+}}\frac{-i}{z}\mathrm{d}z+\int_{\gamma_{\varepsilon}^{+}}E(z)\mathrm{d}z\rightarrow -\pi,\quad\text{当}\ \varepsilon\rightarrow 0.
\]

另一方面,

\[
\begin{split}
\int_{L_1}\frac{1-e^{iz}}{z^2}\mathrm{d}z+\int_{L_2}\frac{1-e^{iz}}{z^2}\mathrm{d}z&=\int_{\varepsilon}^{R}\frac{1-e^{ix}}{x^2}\mathrm{d}x+\int_{-R}^{-\varepsilon}\frac{1-e^{ix}}{x^2}\mathrm{d}x\\
&\stackrel{t=-x}{=}\int_{\varepsilon}^{R}\frac{1-e^{ix}}{x^2}\mathrm{d}x+\int_{R}^{\varepsilon}\frac{1-e^{-it}}{t^2}\cdot(-1)\mathrm{d}t\\
&=\int_{\varepsilon}^{R}\frac{1-e^{ix}}{x^2}\mathrm{d}x+\int_{\varepsilon}^{R}\frac{1-e^{-ix}}{x^2}\mathrm{d}x\\
&=\int_{\varepsilon}^{R}\frac{2-(e^{ix}+e^{-ix})}{x^2}\mathrm{d}x\\
&=2\int_{\varepsilon}^{R}\frac{1-\cos x}{x^2}\mathrm{d}x
\end{split}
\]

最后, 在 $(*)$ 式中令 $R\rightarrow\infty$, $\varepsilon\rightarrow 0$, 得

\[
2\int_{0}^{+\infty}\frac{1-\cos x}{x^2}\mathrm{d}x+(-\pi)=0,
\]

即有

\[
\int_{0}^{+\infty}\frac{1-\cos x}{x^2}\mathrm{d}x=\frac{\pi}{2}.
\]

参考 [1] P.44 Example 2.

[1] Elias M. Stein & Rami Shakarchi,  Complex Analysis.