问题及解答

设正方形 $ABCD$ 的边长为 4, 点 $O$ 是边 $AB$ 的中点. 以 $O$ 为圆心作半径为 2 的半圆, 与以 $D$ 为圆心, 4 为半径的 $1/4$ 圆弧相交于点 $E$. 求阴影部分的面积.

连接 $AE$, $DE$, $OD$, $OE$. 如下图.

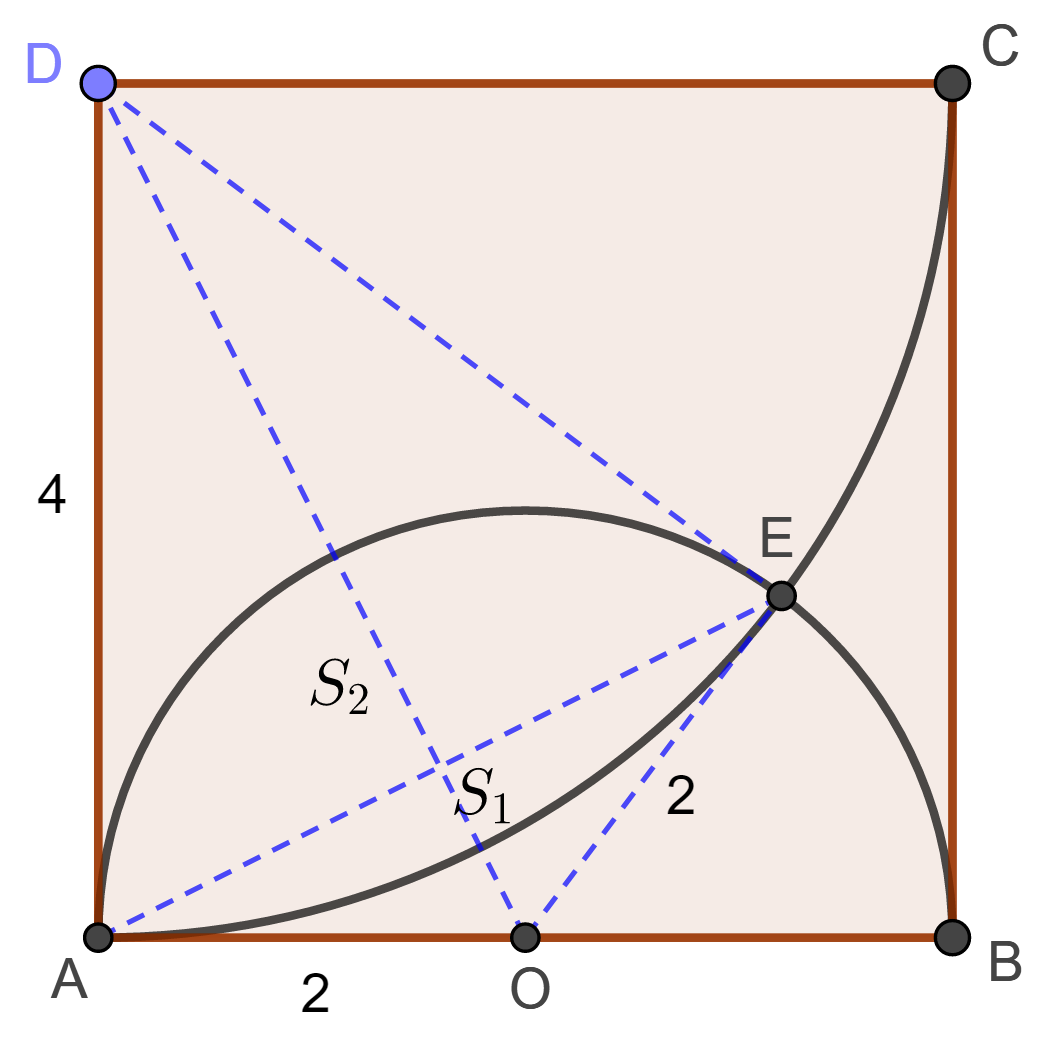
设阴影部分被线段 $AE$ 分为较小和较大两个弓形区域,  它们的面积分别记为 $S_1$, $S_2$. 

容易证明: $DE\perp OE$. （事实上, 由 $OA=OE$, $DA=DE$, $OD=OD$ 知 $\triangle ODA\cong\triangle ODE$.）

记 $\angle OAE=\alpha$, 则 $\angle BOE=\angle ADE=2\alpha$. 且 $\tan\alpha=\frac{1}{2}$.

过 $E$ 作 $EH\perp AB$ 于 $H$. 设 $EH=h$. 在直角三角形 $EOH$ 中, $\angle EOH=2\alpha$.

\[
\tan 2\alpha=\frac{2\tan\alpha}{1-\tan^2\alpha}=\frac{2\times\frac{1}{2}}{1-(\frac{1}{2})^2}=\frac{4}{3}
\]

故可设 $OH=3k$, $h=EH=4k$. 于是 $OE=5k=2$, 得 $k=\frac{2}{5}$. 从而 $h=EH=4k=\frac{8}{5}$. $OH=3k=\frac{6}{5}$.

\[
\begin{split}
S_1&=\text{扇形}DAE-S_{\triangle DAE}=\pi\cdot 4^2\cdot\frac{2\alpha}{2\pi}-\frac{1}{2}AD\cdot AH\\
&=16\alpha-\frac{1}{2}\cdot 4\cdot(2+\frac{6}{5})=16(\alpha-\frac{2}{5})
\end{split}
\]

\[
\begin{split}
S_2&=\text{扇形}OAE-S_{\triangle OAE}=\pi\cdot 2^2\cdot\frac{\pi-2\alpha}{2\pi}-\frac{1}{2}OA\cdot EH\\
&=2(\pi-2\alpha)-\frac{1}{2}\cdot 2\cdot\frac{8}{5}=2\pi-\frac{8}{5}-4\alpha
\end{split}
\]

所以

\[
S_1+S_2=16(\alpha-\frac{2}{5})+(2\pi-\frac{8}{5}-4\alpha)=12\alpha+2\pi-8=12\arctan\frac{1}{2}+2\pi-8.
\]