设圆 $O$ 是 $\triangle ABC$ 的外接圆, $E$, $F$ 分别为边 $AC$, $AB$ 上的点, 使得 $BCEF$ 四点共圆, 圆心为 $J$. $BE$, $CF$ 交于点 $S$, 直线 $JS$ 交圆 $O$ 于点 $T$.
证明: $\angle ATJ=90^\circ$ .
1
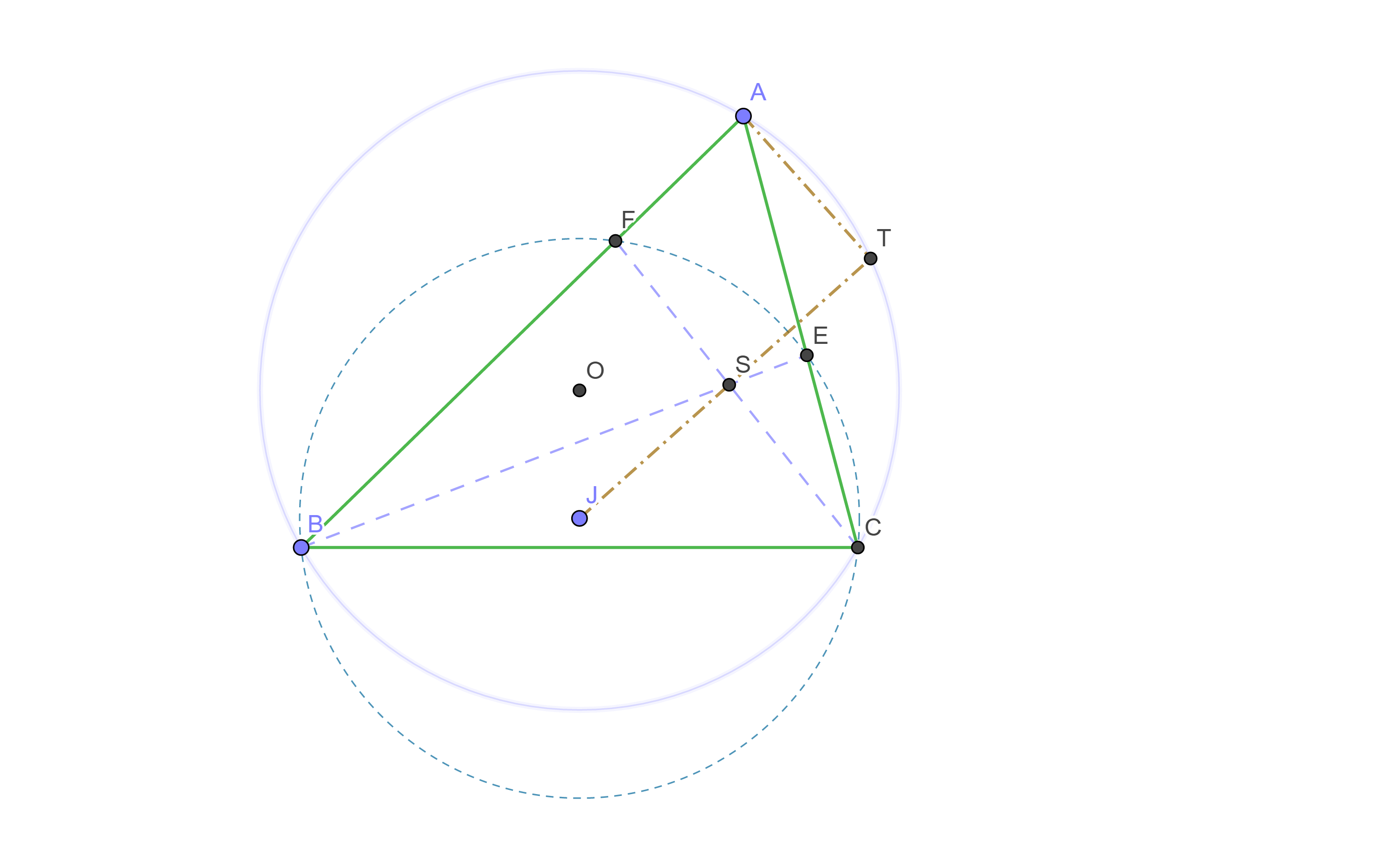
证明: (解析法)
以 $BC$ 所在直线为 $x$ 轴, $BC$ 中垂线为 $y$ 轴建立直角坐标系, 如下图.
设 $|OJ|=1$, $J=(0,t)$, $C=(c,0)$, $A=(a,b)$. 于是 $B=(-c,0)$.
由于 $O$ 为 $\triangle ABC$ 为外接圆圆心, 故 $|OA|=|OC|$. 此推出
\[
\begin{split}
&(a-0)^2+(b-1-t)^2=(c-0)^2+(0-1-t)^2\\
\Rightarrow\ &a^2+b^2-2b(1+t)+(1+t)^2=c^2+(1+t)^2\\
\Rightarrow\ &2b(1+t)=a^2+b^2-c^2.
\end{split}
\]
设 $E=(x_1,y_1)$, $F=(x_2,y_2)$. 直线 $AC$ 和 $AB$ 的方程分别为
\[
\begin{aligned}
\ell_{AC}:\quad& y-0=\frac{b-0}{a-c}(x-c),\\
\ell_{AB}:\quad& y-0=\frac{b-0}{a+c}(x+c).\\
\end{aligned}
\]
故 $y_1=\frac{b}{a-c}(x_1-c)$, $y_2=\frac{b}{a+c}(x_2+c)$.
由于 $B,C,E,F$ 四点共圆, 且所在圆圆心为 $J$, 故 $|EJ|^2=|CJ|^2=|FJ|^2$. 即有
\[
(y_1-t)^2+x_1^2=t^2+c^2=(y_2-t)^2+x_2^2.
\]
这推出
\[
\begin{cases}
y_1^2-2y_1 t+x_1^2=c^2,\\
y_2^2-2y_2 t+x_2^2=c^2.
\end{cases}
\]
将 $y_1$, $y_2$ 的表达式代入, 得
\[
\begin{cases}
\frac{b^2}{(a-c)^2}(x_1-c)-\frac{2b}{a-c}t+x_1+c=0,\\
\frac{b^2}{(a+c)^2}(x_2+c)-\frac{2b}{a+c}t+x_2-c=0.
\end{cases}
\]
解得
\[
\begin{cases}
x_1=\dfrac{2b(a-c)t+b^2 c-c(a-c)^2}{b^2+(a-c)^2},\quad (1)\\
x_2=\dfrac{2b(a+c)t-b^2 c+c(a+c)^2}{b^2+(a+c)^2}.\quad (2)\\
\end{cases}
\]
代入 $y_1$, $y_2$ 的表达式, 求得
\[
\begin{cases}
y_1=b\cdot\dfrac{2bt-2c(a-c)}{b^2+(a-c)^2},\quad(3)\\
y_2=b\cdot\dfrac{2bt+2c(a+c)}{b^2+(a+c)^2}.\quad(4)
\end{cases}
\]
直线 $BE$, $CF$ 的方程分别是
\[
\begin{aligned}
\ell_{BE}:\quad y-0=\frac{y_1-0}{x_1-(-c)}(x-(-c))\quad\Rightarrow\ y=\frac{y_1}{x_1+c}(x+c)\\
\ell_{CF}:\quad y-0=\frac{y_2-0}{x_1-c}(x-c)\quad\Rightarrow\ y=\frac{y_2}{x_2-c}(x-c)
\end{aligned}
\]
联立上述两方程, 求出 $S$ 点坐标.
\[
\begin{split}
&\frac{y_1}{x_1+c}(x+c)=\frac{y_2}{x_2-c}(x-c)\\
\Rightarrow\ & x_S=\dfrac{(\frac{y_1}{x_1+c}+\frac{y_2}{x_2-c})\cdot c}{\frac{y_2}{x_2-c}-\frac{y_1}{x_1+c}}\quad(5)
\end{split}
\]
其中
\[
\begin{aligned}
\frac{y_1}{x_1+c}&=\frac{bt-c(a-c)}{(a-c)t+bc},\\
\frac{y_2}{x_2-c}&=\frac{bt+c(a+c)}{(a+c)t-bc}.
\end{aligned}
\]
从而由 $(5)$ 式, 计算得
\[
x_S=\dfrac{ab(t^2+c^2)}{-bt^2+(b^2+a^2-c^2)t+bc^2}=\dfrac{a(t^2+c^2)}{t^2+2t+c^2}.
\]
这里最后一个等号是将 $b^2+a^2-c^2=2b(1+t)$ 代入化简后所得.
\[
\begin{split}
y_S=\frac{y_1}{x_1+c}(x_S+c)&=\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\biggl(\dfrac{a(t^2+c^2)}{t^2+2t+c^2}+c\biggr)\\
&=\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\frac{(a+c)(t^2+c^2)+2ct}{t^2+2t+c^2}
\end{split}
\]
我们只要证明 $J$, $S$, $D$ 共线. 这里 $D$ 是 $A$ 关于 $O$ 的对称点. 由 $J=(0,t)$, $O=(0,1+t)$, 得 $D=(-a,2(1+t)-b)$.
\[
k_{JD}=\frac{t-(2(1+t)-b)}{0-(-a)}=\frac{b-t-2}{a}.
\]
\[
\begin{split}
k_{JS}&=\frac{y_S-y_J}{x_S-x_J}=\frac{y_S-t}{x_S}\\
&=\dfrac{\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\frac{(a+c)(t^2+c^2)+2ct}{t^2+2t+c^2}-t}{\frac{a(t^2+c^2)}{t^2+2t+c^2}}\\
&=\dfrac{\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\Bigl((a+c)(t^2+c^2)+2ct\Bigr)-t(t^2+2t+c^2)}{a(t^2+c^2)}\\
&=\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\biggl[\frac{(a+c)(t^2+c^2)+2ct}{a(t^2+c^2)}\biggr]-\frac{t}{a}\cdot\frac{t^2+2t+c^2}{t^2+c^2}\\
&=\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\biggl[\frac{a+c}{a}+\frac{2ct}{a(t^2+c^2)}\biggr]-\frac{t}{a}\cdot\biggl[1+\frac{2t}{t^2+c^2}\biggr]\\
&=\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\frac{a+c}{a}+\frac{bt-c(a-c)}{(a-c)t+bc}\cdot\frac{2ct}{a(t^2+c^2)}-\frac{t}{a}-\frac{2t^2}{a(t^2+c^2)}\\
&=\frac{1}{a}\cdot\biggl[\frac{bt-c(a-c)}{(a-c)t+bc}\cdot(a+c)-t\biggr]+\frac{2t}{a(t^2+c^2)}\biggl[\frac{bt-c(a-c)}{(a-c)t+bc}\cdot c-t\biggr]\\
&=\frac{1}{a}\cdot\frac{b(a+c)t-c(a^2-c^2)-(a-c)t^2-bct}{(a-c)t+bc}+\frac{2t}{a(t^2+c^2)}\cdot\frac{bct-c^2(a-c)-(a-c)t^2-bct}{(a-c)t+bc}\\
&=\frac{1}{a}\cdot\frac{bat-c(a^2-c^2)-(a-c)t^2}{(a-c)t+bc}+\frac{2t}{a}\cdot\frac{-(a-c)}{(a-c)t+bc}\\
&=\frac{-(a-c)t^2+\bigl(ba-2(a-c)\bigr)t-c(a^2-c^2)}{a\bigl[(a-c)t+bc\bigr]}.
\end{split}
\]
于是
\[
\begin{split}
&k_{JS}=k_{JD}\\
\Rightarrow &\ \frac{-(a-c)t^2+\bigl(ba-2(a-c)\bigr)t-c(a^2-c^2)}{a\bigl[(a-c)t+bc\bigr]}=\frac{b-t-2}{a}\\
\Rightarrow &\ -(a-c)t^2+\bigl[ba-2(a-c)\bigr]t-c(a^2-c^2)=\bigl[(a-c)t+bc\bigr]\cdot(b-t-2)\\
\Rightarrow &\ \bigl[ba-2(a-c)\bigr]t-c(a^2-c^2)=b(a-c)t-2(a-c)t+b^2c-bct-2bc\\
\Rightarrow &\ bat-2(a-c)t-c(a^2-c^2)=bat-2bct-2(a-c)t+b^2 c-2bc\\
\Rightarrow &\ -c(a^2-c^2)=-2bct+b^2 c-2bc\\
\Rightarrow &\ 2bt=a^2-c^2+b^2-2b\\
\Rightarrow &\ 2b(1+t)=a^2+b^2-c^2.
\end{split}
\]
得证.