问题

Floyd 算法是图论中计算两两顶点之间最短路径的算法. 算法复杂度为 $O(N^3)$.

设 $G=(V,E)$ 是一个带权图(有向或者无向). $n=|V|$, $W$ 是它的权矩阵. 顶点集合 $V=\{v_1,v_2,\ldots,v_n\}$, 有时不妨记为 $V=\{1,2,\ldots,n\}$.

通过下面的算法计算距离矩阵 $D=(d_{ij})_{n\times n}$ 和路径矩阵 $R=(r_{ij})_{n\times n}$.

其中 $d_{ij}=\text{dist}(v_i,v_j)$. 而 $r_{ij}$ 表示顶点 $v_i$ 到 $v_j$ 的最短路径中经过的某个顶点.

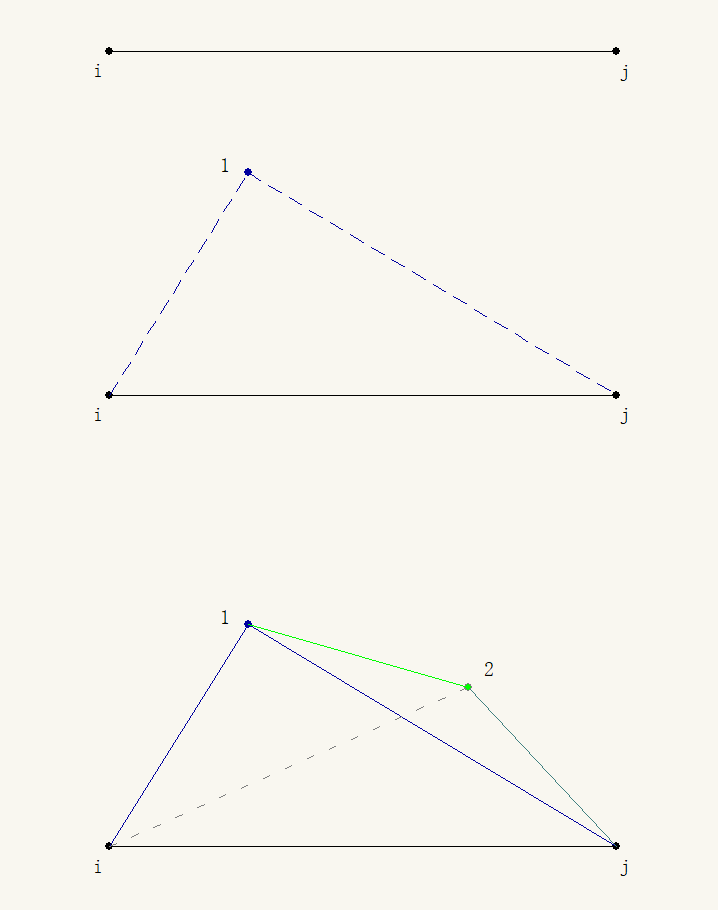
（1）第一幅图. 线段 $i--j$

$d_{ij}^{(0)}=d(i,j)$ 指顶点 $v_i$ 和 $v_j$ 之间的权, 初始矩阵 $D^{(0)}=(d_{ij}^{(0)})=W$.

(2) 第二幅图. 三角形 $ij1$. 在 $v_i$ 和 $v_j$ 之间插入了顶点 $v_1$.

\[
d_{ij}^{(1)}=\min\{d_{ij}^{(0)},d_{i1}^{(0)}+d_{1j}^{(0)}\}
\] 

也就是说, 从 $v_i$ 到 $v_j$ 的最短路径必从三角形 $ij1$ 的边界(boundary)上经过.

(3) 第三幅图. 四面体 $ij12$（也就是三维单形）

从 $v_i$ 到 $v_j$ 的最短路径, 先考虑从 $\triangle i21$ 的边界(boundary)经过, 然后从 $\triangle 2j1$ 的边界(boundary)经过. 将它们的和与 $d_{ij}^{(1)}$ 作比较. 取长度较小的路径.

实际上, 从 $v_i$ 到 $v_j$ 的最短路径, 必从四面体 $ij12$ 的三个面 $i21$, $2j1$, $ij1$ 所组成的复形的骨架上经过. 当然这样的话, 已经将三角形 $ij2$ 的边界考虑了. 因此, 从 $v_i$ 到 $v_j$ 的最短路径必从四面体 $ij12$ 的边界上经过.

其余的, 可从高维上类似理解.

以下是 MATLAB 代码

% page 93.
% filename: floyd.m
function [D,R] = floyd(A)
n=size(A,1); % n 等于矩阵 A 的行数.
D=A
for i=1:n
    for j=1:n
        R(i,j)=j;
    end
end
R

for k=1:n
    for i=1:n
        for j=1:n
            if D(i,k)+D(k,j) < D(i,j)
                D(i,j)=D(i,k)+D(k,j);
                R(i,j)=R(i,k);
            end
        end
    end
    k
    D
    R
    '-----------------------'
end

注意:

• $k$ 是指插入点的标号, 因此关于 $k$ 的循环一定要放在最外层.
• 其中的 R(i,j)=R(i,k); 也可以换成 R(i,j)=k; 但是要注意, 如果是用C/C++编程, 那么指标 k 从0 开始的, 因此必须要前后一致.