过正三角形 $ABC$ 中一点 $P$ 作三条边的垂线, 分别交边 $BC$, $CA$, $AB$ 于 $D,E,F$ 三点. 已知 $|AF|=7\text{cm}$, $|BD|=8\text{cm}$, $|CE|=10\text{cm}$. 求正三角形 $ABC$ 的边长.
Remark:
题目来源：Lei LIU
1
首先给出 David CHEN 的解答.
如下图, 作若干辅助线.
由 $|GC|=2|CE|=2\times 10=20$, 得
\[
\begin{split}
20&=|GD|+|DC|=|GD|+|DH|-|HC|\\
&=2|GD|-|HC|=2|GB|+16-|KC|,
\end{split}
\]
这推出 $2|GB|-|KC|=4$. 记为 (1) 式.
由 $|AK|=2|AF|=2\times 7=14$, 得
\[
\begin{split}
14&=|AK|=|AE|+|EK|\\
&=|AL|+|LE|+|EK|\\
&=|AL|+2|EK|\\
&=|AL|+2(|EC|-|KC|)\\
&=|AL|+20-2|KC|,
\end{split}
\]
这推出 $2|KC|-|AL|=6$. 记为 (2) 式.
由 $|BI|=2|BD|=2\times 8=16$, 得
\[
\begin{split}
16&=|BI|=|IF|+|BF|=|IF|+|FJ|+|BJ|\\
&=2|IF|+|BJ|\\
&=2(|AF|+|AI|)+|BJ|\\
&=14+2|AL|+|GB|,
\end{split}
\]
这推出 $2|AL|+|GB|=2$. 记为 (3) 式.
以上三个式子 (1) (2) (3) 联立, 可求出各个线段的长.
\[
\begin{cases}
2|GB|-|KC|=4,\\
2|KC|-|AL|=6,\\
2|AL|+|GB|=2.
\end{cases}
\]
解得 $|GB|=\frac{10}{3}$, $|KC|=\frac{8}{3}$, $|AL|=-\frac{2}{3}$.
因此, $|BC|=|GC|-|GB|=20-\frac{10}{3}=\frac{50}{3}$.
2
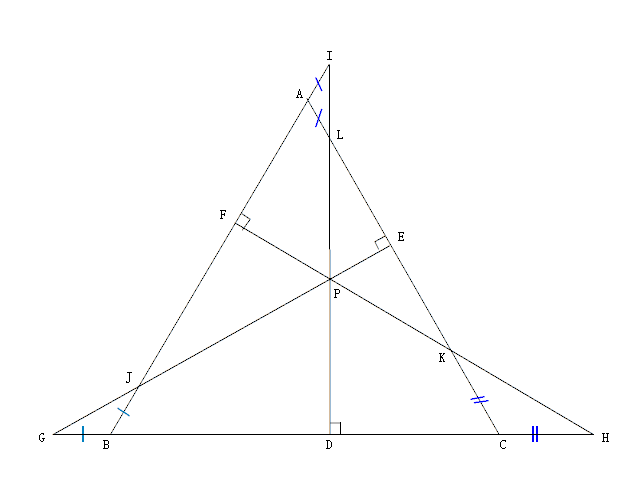
（法二）
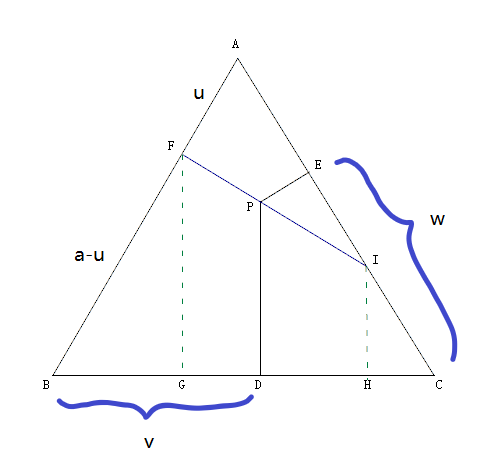
记 $|AF|=u$, $|BD|=v$, $|CE|=w$. 设正三角形的边长为 $a$.
则 $|BG|=\frac{1}{2}|BF|=\frac{1}{2}(a-u)$. $|CH|=\frac{1}{2}|CI|=\frac{1}{2}(a-2u)$.
\[
|GF|=\frac{\sqrt{3}}{2}(a-u),\quad |HI|=\frac{\sqrt{3}}{2}(a-2u).
\]
记 $|HJ|=h$, $|DP|=\ell$. 注意到 $|GD|=v-\frac{1}{2}(a-u)$,
\[
|GH|=a-|BG|-|CH|=a-\frac{1}{2}(a-u)-\frac{1}{2}(a-2u)=\frac{3}{2}u.
\]
下面利用相似三角形计算 $h$. 在三角形 $FGJ$ 中, $\frac{|HI|}{|HJ|}=\frac{|GF|}{|GJ|}$, 得
\[
\frac{\frac{\sqrt{3}}{2}(a-2u)}{h}=\frac{\frac{\sqrt{3}}{2}(a-u)}{\frac{3}{2}u+h},
\]
\[
\begin{split}
\Rightarrow &(a-2u)(\frac{3}{2}u+h)=(a-u)h\\
\Rightarrow &\frac{3}{2}au+ah-3u^2-2uh=ah-uh\\
\Rightarrow &\frac{3}{2}au-3u^2=uh\\
\Rightarrow & h=\frac{3}{2}a-3u.
\end{split}
\]
计算 $\ell=|PD|$. 由 $\frac{|HI|}{|HJ|}=\frac{|PD|}{|DJ|}$, 得
\[
\frac{\frac{\sqrt{3}}{2}(a-2u)}{h}=\frac{\ell}{h+\frac{3}{2}u-(v-\frac{1}{2}(a-u))}.
\]
推出
\[
\begin{split}
|PD|=\ell&=\frac{1}{h}\biggl[\frac{\sqrt{3}}{2}(a-2u)\Bigl(h+\frac{3}{2}u-v+\frac{1}{2}(a-u)\Bigr)\biggr]\\
&=\frac{1}{3(\frac{1}{2}a-u)}\cdot\frac{\sqrt{3}}{2}(a-2u)\Bigl(\frac{3}{2}a-3u+\frac{3}{2}u-v+\frac{1}{2}a-\frac{1}{2}u\Bigr)\\
&=\frac{1}{\sqrt{3}}(2a-2u-v).
\end{split}
\]
计算 $|PF|$.
由 $\frac{|PF|}{|FI|}=\frac{|GD|}{|GH|}$, 得
\[
\frac{|PF|}{\sqrt{3}u}=\frac{v-\frac{1}{2}(a-u)}{\frac{3}{2}u},
\]
这推出
\[
|PF|=\sqrt{3}\cdot\frac{v-\frac{1}{2}(a-u)}{\frac{3}{2}}=\frac{2}{\sqrt{3}}(v-\frac{1}{2}(a-u)).
\]
计算 $|PE|$, 注意到 $|PE|=\frac{1}{2}|PI|$, 所以先计算 $|PI|$.
由 $\frac{|PI|}{|FI|}=\frac{|DH|}{|GH|}$, 得
\[
\frac{|PI|}{\sqrt{3}u}=\frac{\frac{3}{2}u-(v-\frac{1}{2}(a-u))}{\frac{3}{2}u},
\]
这推出
\[
|PI|=\frac{2}{\sqrt{3}}\Bigl[\frac{3}{2}u-v+\frac{1}{2}a-\frac{1}{2}u\Bigr]=\frac{2}{\sqrt{3}}(u-v+\frac{1}{2}a).
\]
因此
\[
|PE|=\frac{1}{2}|PI|=\frac{1}{\sqrt{3}}(u-v+\frac{1}{2}a).
\]
当然, 我们可以顺带算一下 $|PD|+|PE|+|PF|$ 是否是常数.
\[
|PD|+|PE|+|PF|=\frac{1}{\sqrt{3}}(2a-2u-v)+\frac{1}{\sqrt{3}}(u-v+\frac{1}{2}a)+\frac{2}{\sqrt{3}}(v-\frac{1}{2}(a-u))=\frac{\sqrt{3}}{2}a.
\]
NOTE: 这和 $|PD|+|PE|+|PF|=\frac{2S}{a}$ 并不矛盾, 这里 $S$ 是正三角形 $ABC$ 的面积. 因为 $S=\frac{\sqrt{3}}{4}a^2$.
下面将 $u=7$, $v=8$ 代入.
\[
\begin{aligned}
|PD|=\frac{1}{\sqrt{3}}(2a-2u-v)=\frac{1}{\sqrt{3}}(2a-22),\\
|PE|=\frac{1}{\sqrt{3}}(u-v+\frac{1}{2}a)=\frac{1}{\sqrt{3}}(\frac{1}{2}a-1),\\
|PF|=\frac{2}{\sqrt{3}}(v-\frac{1}{2}(a-u))=\frac{2}{\sqrt{3}}(\frac{23}{2}-\frac{1}{2}a).
\end{aligned}
\]
于是
\[
\begin{split}
w&=|CE|=|CI|+|IE|\\
&=(a-2u)+\sqrt{3}|PE|\\
&=(a-2u)+\sqrt{3}\cdot\frac{1}{\sqrt{3}}(u-v+\frac{1}{2}a)\\
&=\frac{3}{2}a-u-v.
\end{split}
\]
将 $w=10$ 代入, 于是有
\[
10=\frac{3}{2}a-7-8\quad\Rightarrow\quad a=\frac{50}{3}.
\]
一般的, 有
\[
\frac{3}{2}a=u+v+w,
\]
即
\[
a=\frac{2}{3}(u+v+w)=\frac{2}{3}(|AF|+|BD|+|CE|).
\]
特别的, 根据对称性,
\[
a=\frac{2}{3}(|AE|+|CD|+|BF|).
\]
Remark: 如果已经知道 $a$ 与 $u+v+w$ 之间存在线性关系, 即假设 $a=k(u+v+w)$. 加上对称性, 也应满足 $a=k\bigl((a-u)+(a-v)+(a-w)\bigr)$. 从而容易求出 $k=\frac{3}{2}$.