一维弹性碰撞问题
一维弹性碰撞问题
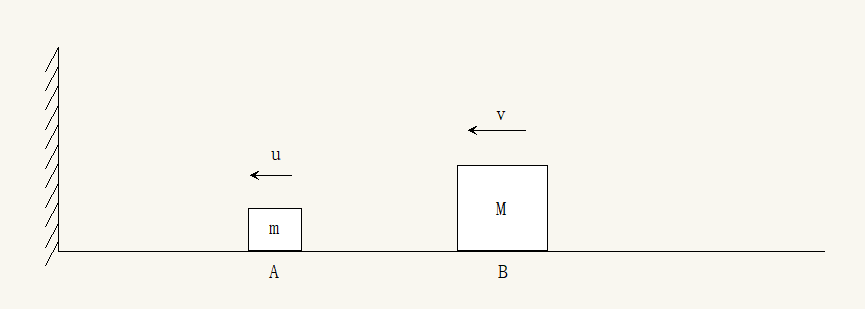
光滑水平面上有两个弹性小方块, $A$ 和 $B$. 左侧有堵墙. 这两个小方块的质量分别为 $m$, $M$, 单位: $\mathrm{kg}$. $A$ 的初速为0. $B$ 初速度为 $v$, 方向向左, 向 $A$ 撞去. (这里不考虑摩檫力, 小方块 $A$ 被墙反弹后, 能量不损失. 不考虑撞墙刹那的速度变化过程, 如果碰撞前速度为 $u$, 则碰撞后速度为 $-u$.)
如果 $m=M=1\mathrm{kg}$, 则小方块 $A$ 共碰撞 3 次.
如果 $m=1\mathrm{kg}$, $M=100\mathrm{kg}$, 则小方块 $A$ 共碰撞 31 次.
如果 $m=1\mathrm{kg}$, $M=10000\mathrm{kg}$, 则小方块 $A$ 共碰撞 314 次.
如果 $m=1\mathrm{kg}$, $M=1000000\mathrm{kg}$, 则小方块 $A$ 共碰撞 3141 次.
如果 $m=1\mathrm{kg}$, $M=100000000\mathrm{kg}$, 则小方块 $A$ 共碰撞 31415 次.
$\vdots$
我们看到碰撞次数与 $\pi=3.1415926\cdots$ 有关.
请问背后的原理是什么?
Remark:
小方块 $A$ 与 $B$ 和墙的碰撞都计算在内.
问题来源: 转发自 Q. X. Dong