问题及解答

假设正方形的边长是 10, 求图中绿色部分的面积.

Answer:  单个的绿色部分面积为

\[25\arccos\frac{1}{2\sqrt{2}}-100\arccos\frac{5}{4\sqrt{2}}+\frac{25}{2}\sqrt{7}\]

题目来源: Lei Liu (刘磊)

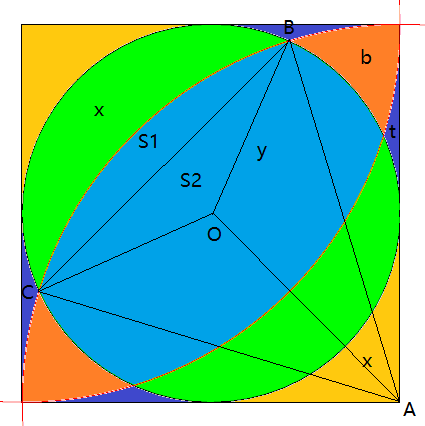
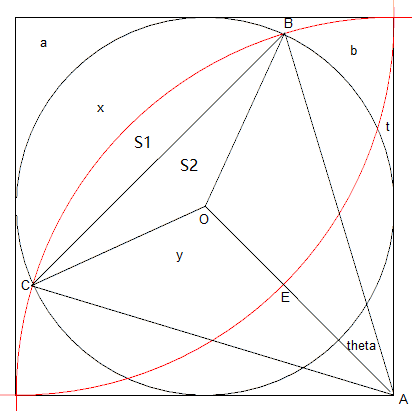
我们不妨假设正方形边长是 $2r$. 于是, $|OA|=\sqrt{2}r$, $|OB|=r$, $|AB|=2r$.

记 $\angle OAB=\theta$, $\angle AOB=\pi-\alpha$. 于是根据余弦定理, 得

\[
\cos\theta=\frac{|OA|^2+|AB|^2-|OB|^2}{2|OA|\cdot|AB|}=\frac{(\sqrt{2}r)^2+(2r)^2-r^2}{2\sqrt{2}r\cdot 2r}=\frac{5}{4\sqrt{2}},
\]

\[
\cos(\pi-\alpha)=\frac{|OA|^2+|OB|^2-|AB|^2}{2|OA|\cdot|OB|}=\frac{(\sqrt{2}r)^2+r^2-(2r)^2}{2\sqrt{2}r\cdot r}=-\frac{1}{2\sqrt{2}}.
\]

即有 $\cos\theta=\frac{5}{4\sqrt{2}}$, $\cos\alpha=\frac{1}{2\sqrt{2}}$, $\sin\theta=\frac{\sqrt{7}}{4\sqrt{2}}$, $\sin\alpha=\frac{\sqrt{7}}{2\sqrt{2}}$.

这推出 $\theta=\arccos\frac{5}{4\sqrt{2}}$, $\alpha=\arccos\frac{1}{2\sqrt{2}}$.

下面计算绿色部分 $x$ 的面积.

\[
x=\text{圆O中扇形 OBC 的面积}-S_1-S_2
\]

其中

\[
\begin{aligned}
S_1&=\pi(2r)^2\cdot\frac{2\theta}{2\pi}-2r\sin\theta\cdot 2r\cos\theta=4r^2\theta-4r^2\sin\theta\cos\theta,\\
S_2&=r\sin\alpha\cdot r\cos\alpha=r^2\sin\alpha\cos\alpha
\end{aligned}
\]

因此,

\[
\begin{split}
x&=\pi r^2\cdot\frac{2\alpha}{2\pi}-(4r^2\theta-4r^2\sin\theta\cos\theta)-r^2\sin\alpha\cos\alpha\\
&=(\alpha -4\theta+4\sin\theta\cos\theta-\sin\alpha\cos\alpha)r^2\\
&=(\arccos\frac{1}{2\sqrt{2}}-4\arccos\frac{5}{4\sqrt{2}}+4\cdot\frac{\sqrt{7}}{4\sqrt{2}}\cdot\frac{5}{4\sqrt{2}}-\frac{\sqrt{7}}{2\sqrt{2}}\cdot\frac{1}{2\sqrt{2}})r^2\\
&=(\arccos\frac{1}{2\sqrt{2}}-4\arccos\frac{5}{4\sqrt{2}}+\frac{\sqrt{7}}{2})r^2
\end{split}
\]

将 $r=5$ 代入, 得

\[
x=25\arccos\frac{1}{2\sqrt{2}}-100\arccos\frac{5}{4\sqrt{2}}+\frac{25\sqrt{7}}{2}.
\]

也可以通过积分计算面积.