设 $AD$ 是 $\triangle ABC$ 的一条中线. $BE$, $CF$ 与 $AD$ 交于一点. 连接 $EF$, 证明: $EF\parallel BC$.
【扩展问题1】
现在假设点 $P$ 在平行于底边 $BC$ 的一条直线上移动, $P$ 在 $\triangle ABC$ 内部. $AD$, $BE$, $CF$ 始终交于点 $P$.
问: 是否仅当 $D$ 是 $BC$ 中点时, 才有 $EF\parallel BC$ ?
【扩展问题2】
记 $\triangle DEF$ 的面积为 $S$. 问: 点 $P$ 在什么位置时, $S$ 取得最值?
1
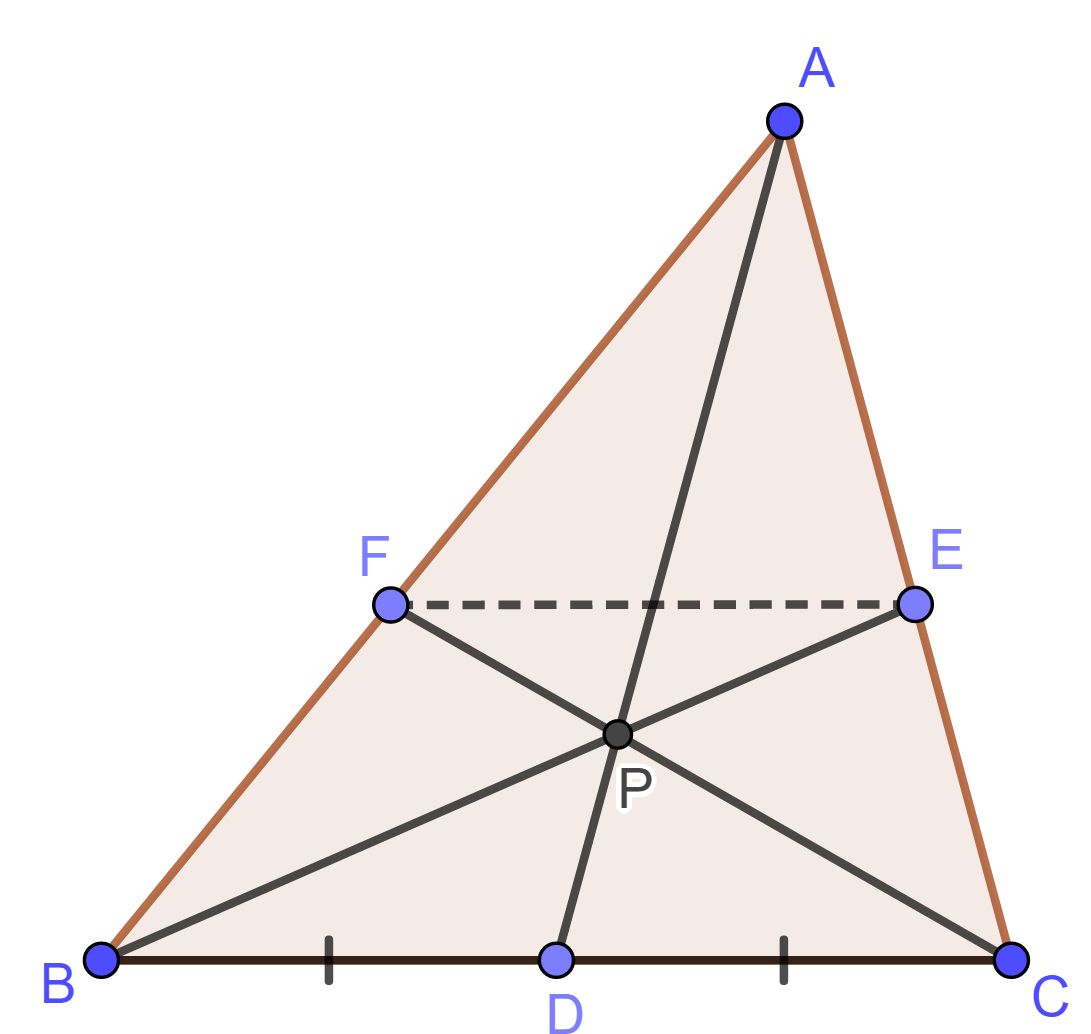
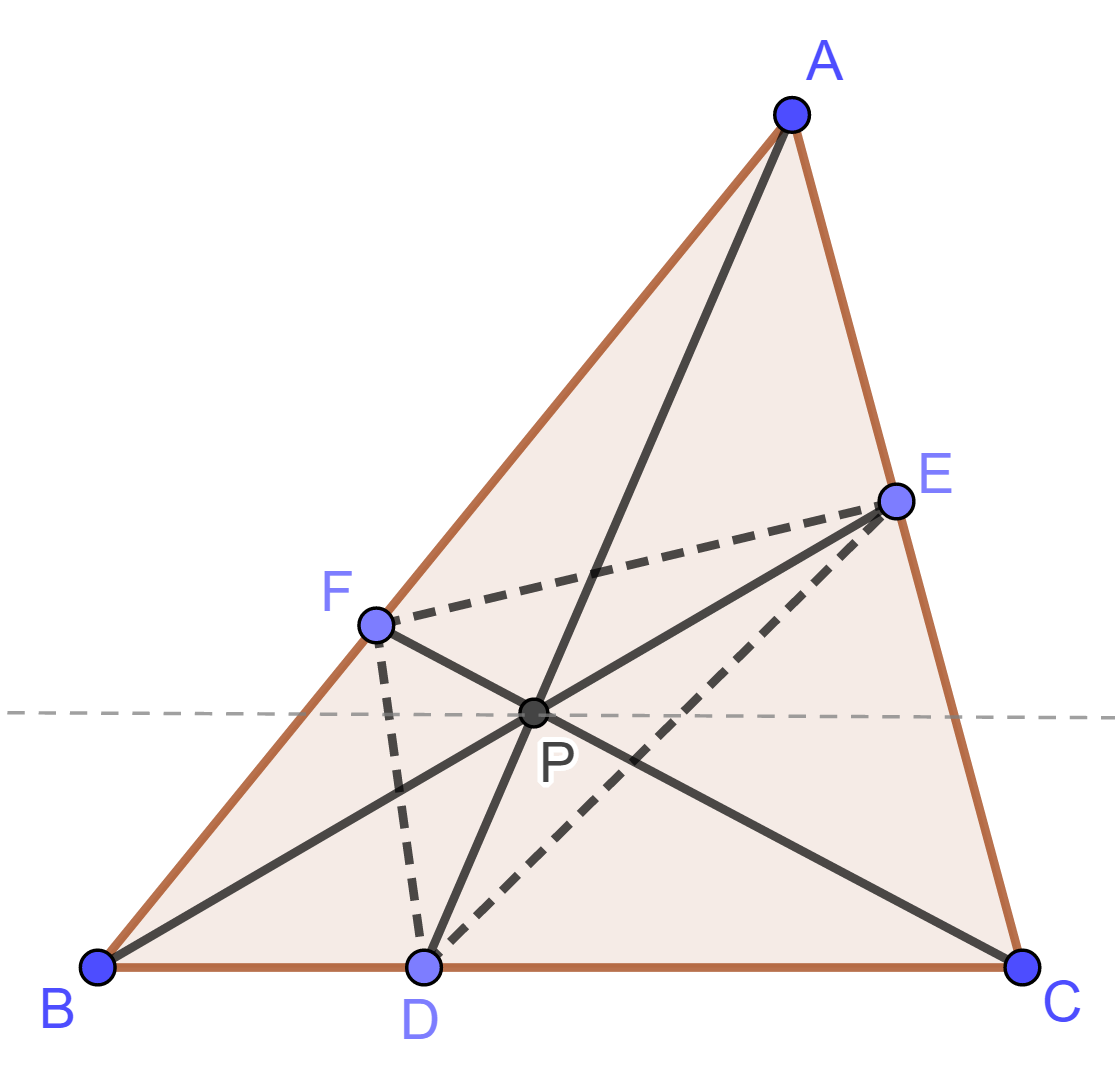
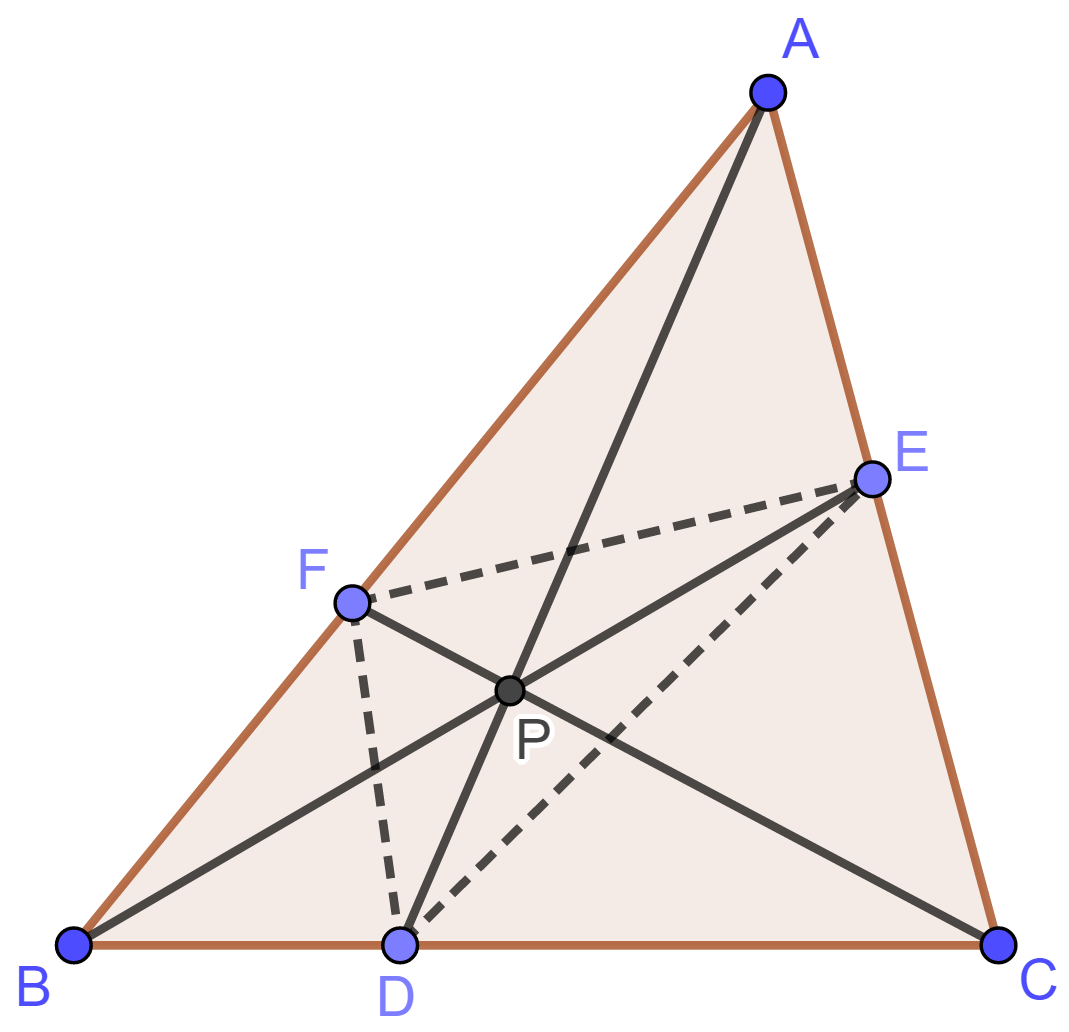
假设 $AD$, $BE$, $CF$ 交于点 $P$. 取 $BF$ 中点 $G$, $CE$ 中点 $H$. 连接 $DG$ 和 $DH$.
由于 $D$ 是 $BC$ 中点, 故 $DG\parallel CF$, 且 $DH\parallel BE$.
\[
\begin{aligned}
DG\parallel CF\quad &\Rightarrow\quad\dfrac{AF}{AG}=\dfrac{AP}{AD},\\
DH\parallel BE\quad &\Rightarrow\quad\dfrac{AE}{AH}=\dfrac{AP}{AD}.\\
\end{aligned}
\]
因此, 推出 $\dfrac{AF}{AG}=\dfrac{AE}{AH}$. 此即
\[
\begin{split}
&\frac{AG}{AF}=\frac{AH}{AE}\\
\Rightarrow\ &\frac{AF+FG}{AF}=\frac{AE+EH}{AE}\\
\Rightarrow\ &\frac{FG}{AF}=\frac{EH}{AE}\\
\Rightarrow\ &\frac{2FG}{AF}=\frac{2EH}{AE}\\
\Rightarrow\ &\frac{BF}{AF}=\frac{CE}{AE}\\
\Rightarrow\ &\frac{AF}{AB}=\frac{AE}{AC}\\
\Rightarrow\ &EF\parallel BC.
\end{split}
\]