1. 证明圆内接四边形的面积公式.
Posted by haifeng on 2025-04-20 09:49:08 last update 2025-04-20 09:52:17 | Answers (1) | 收藏
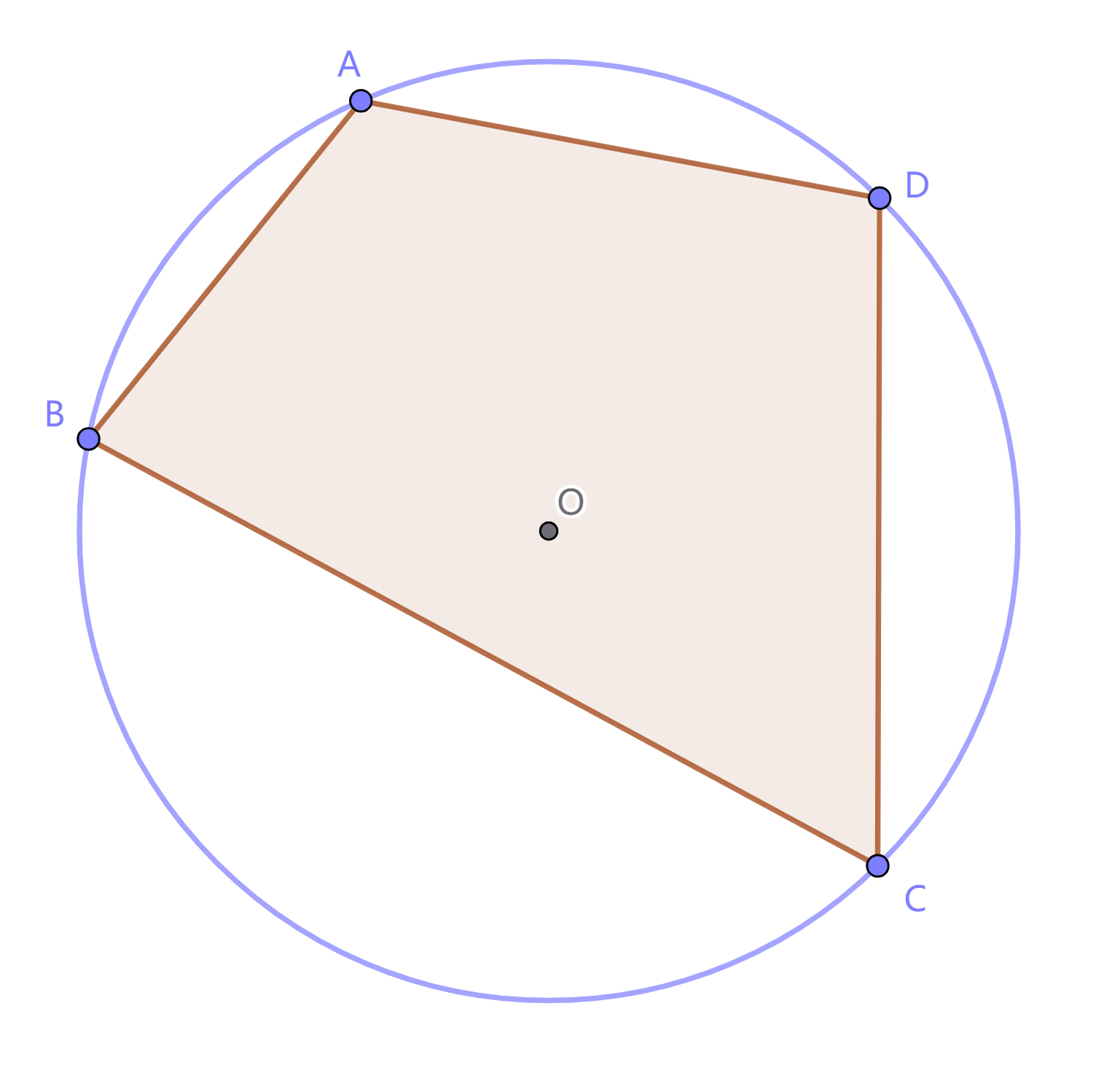
设 $ABCD$ 是圆 $O$ 的内接四边形, 四条边的长度分别为 $|AB|=a$, $|BC|=b$, $|CD|=c$, $|DA|=d$. 若 $p$ 是其周长的一半, 即 $p=\frac{1}{2}(a+b+c+d)$, 则 $ABCD$ 的面积为
\[
S=\sqrt{(p-a)(p-b)(p-c)(p-d)}.
\]