11. 有内接圆的梯形
Posted by haifeng on 2021-01-26 16:14:24 last update 2021-01-26 16:15:26 | Answers (0) | 收藏
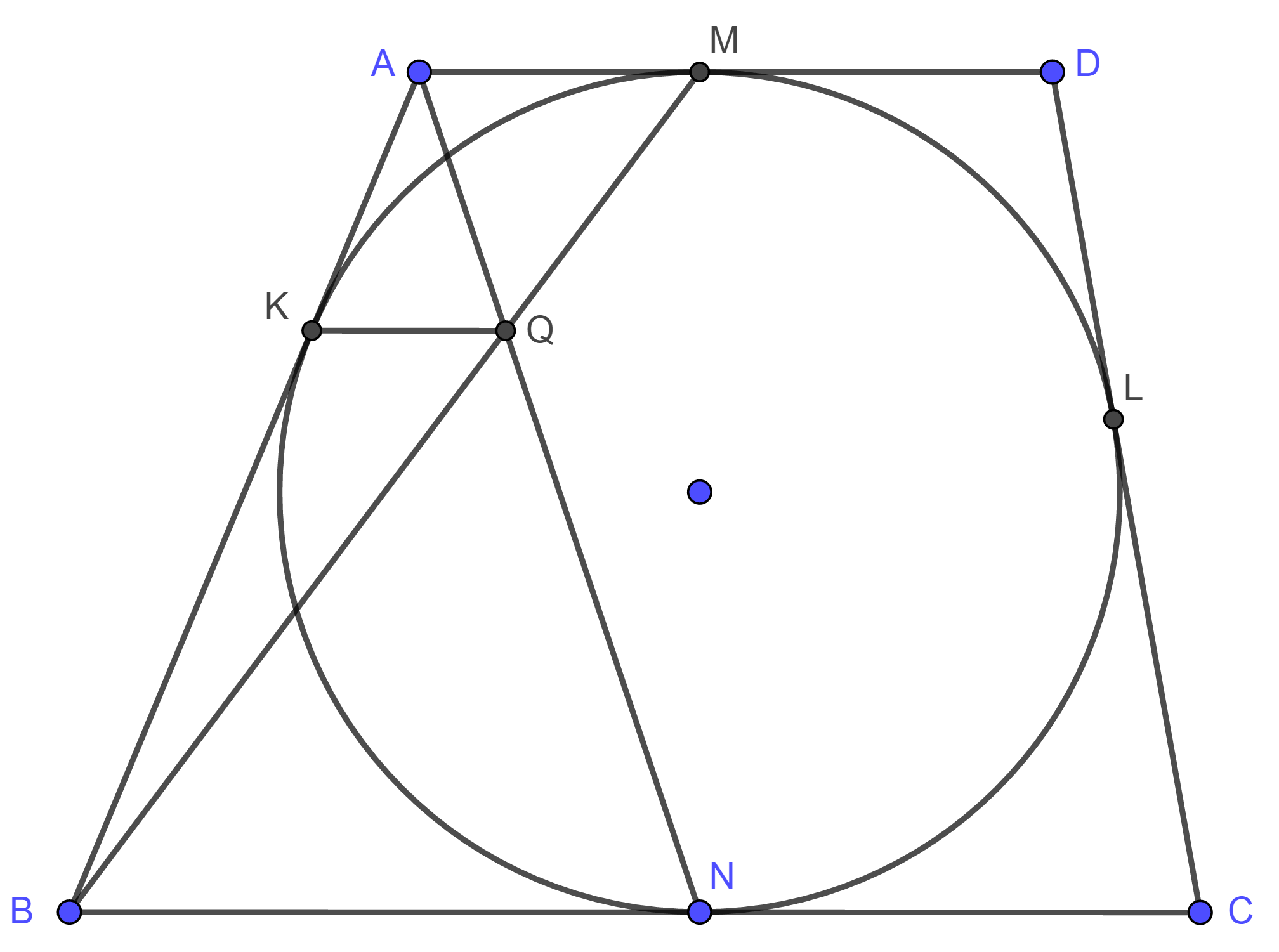
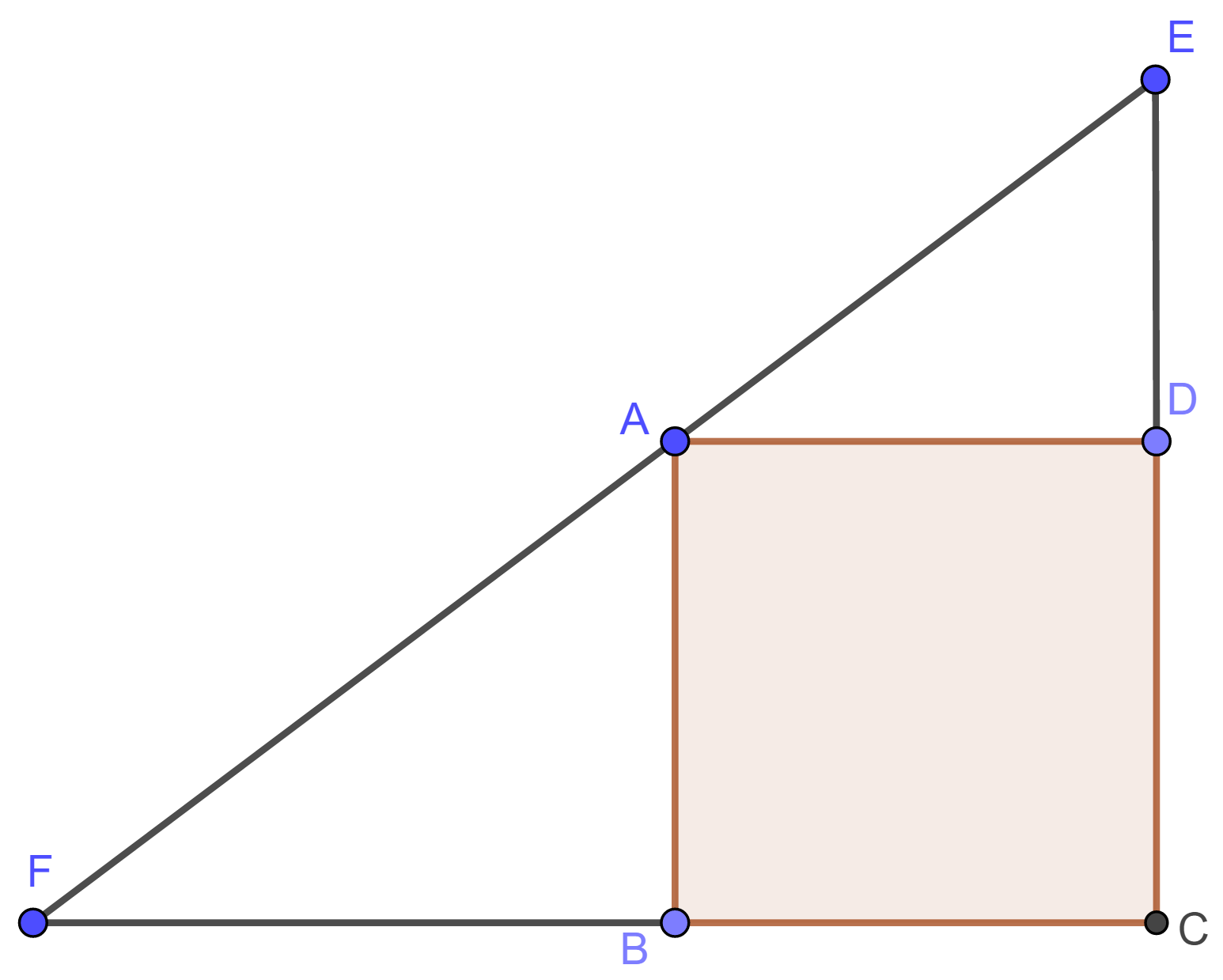
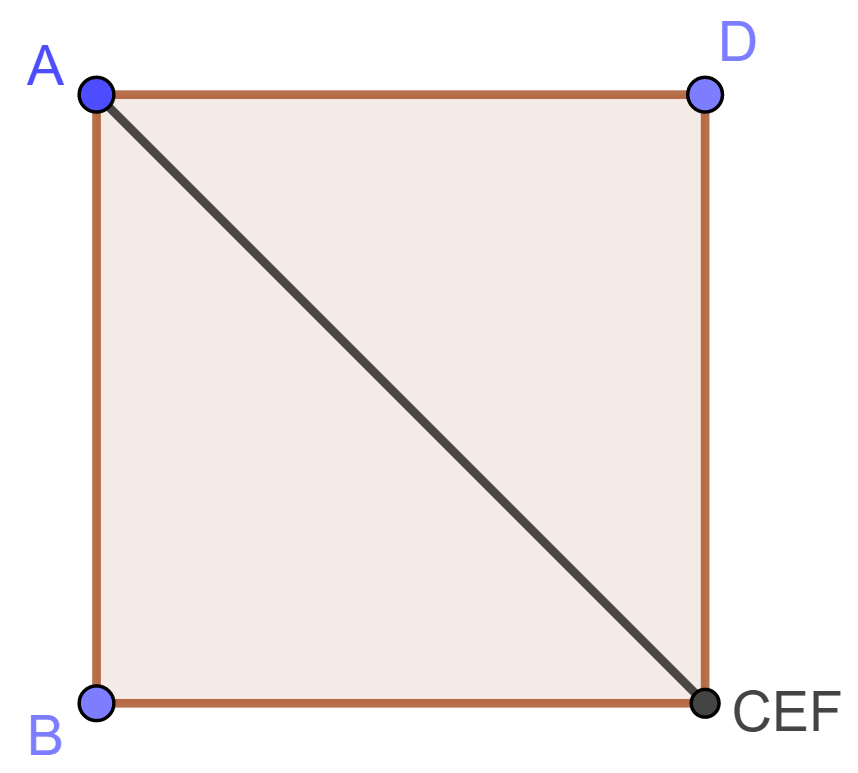
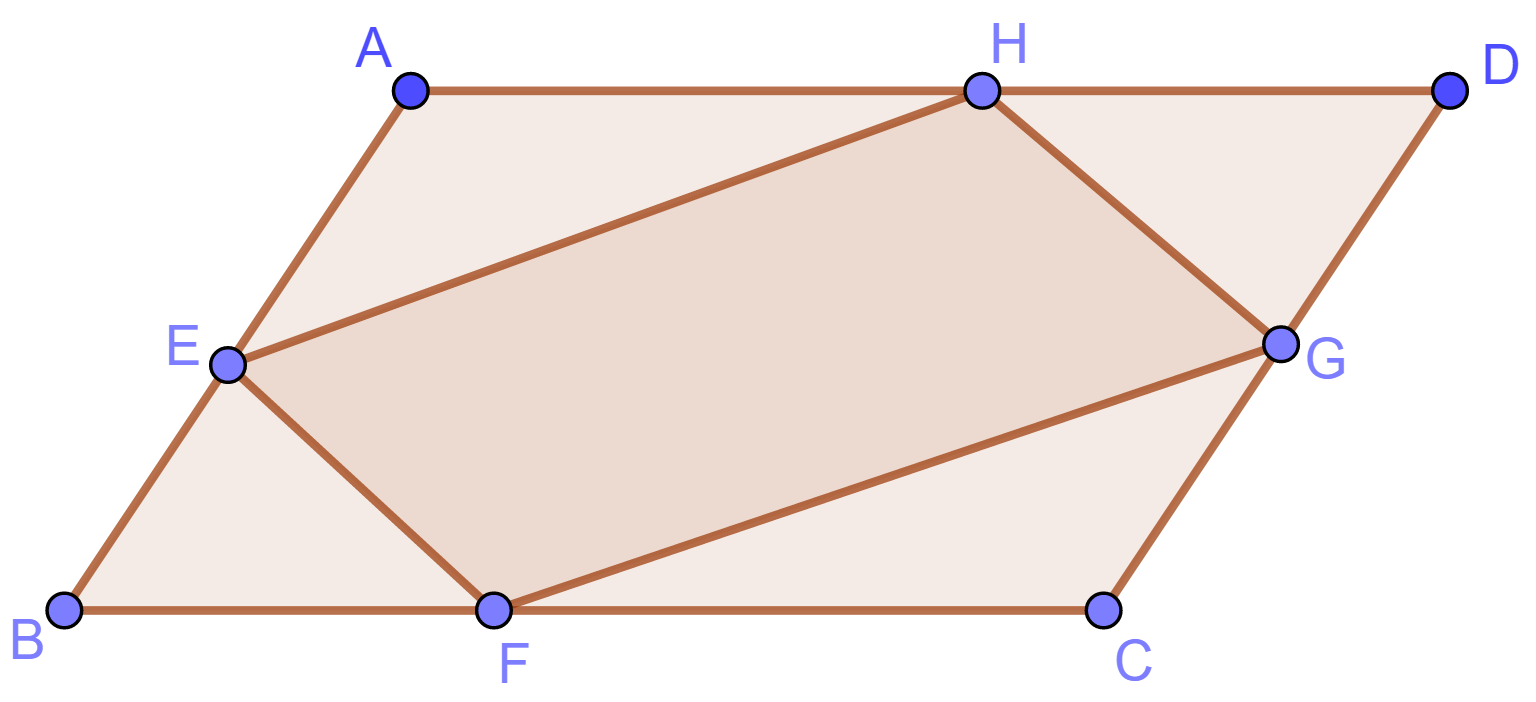
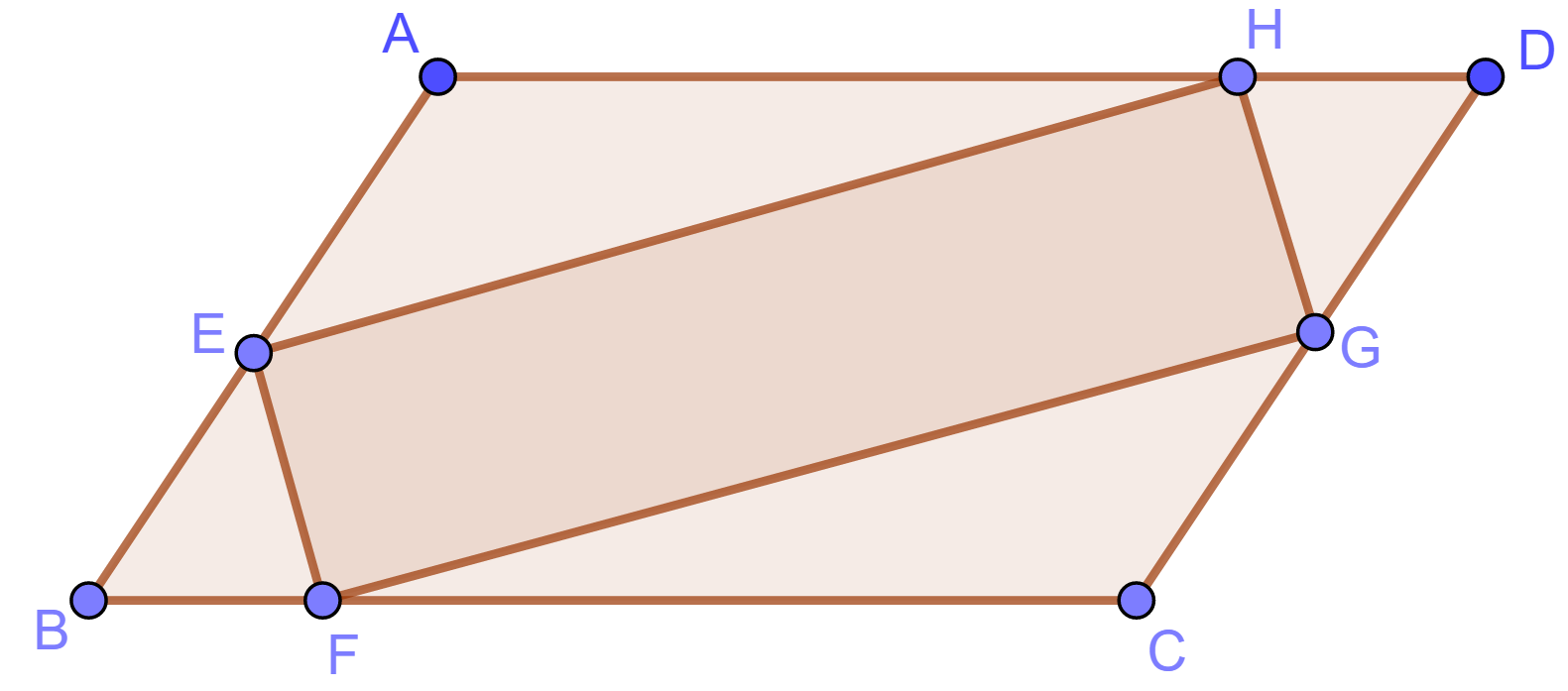
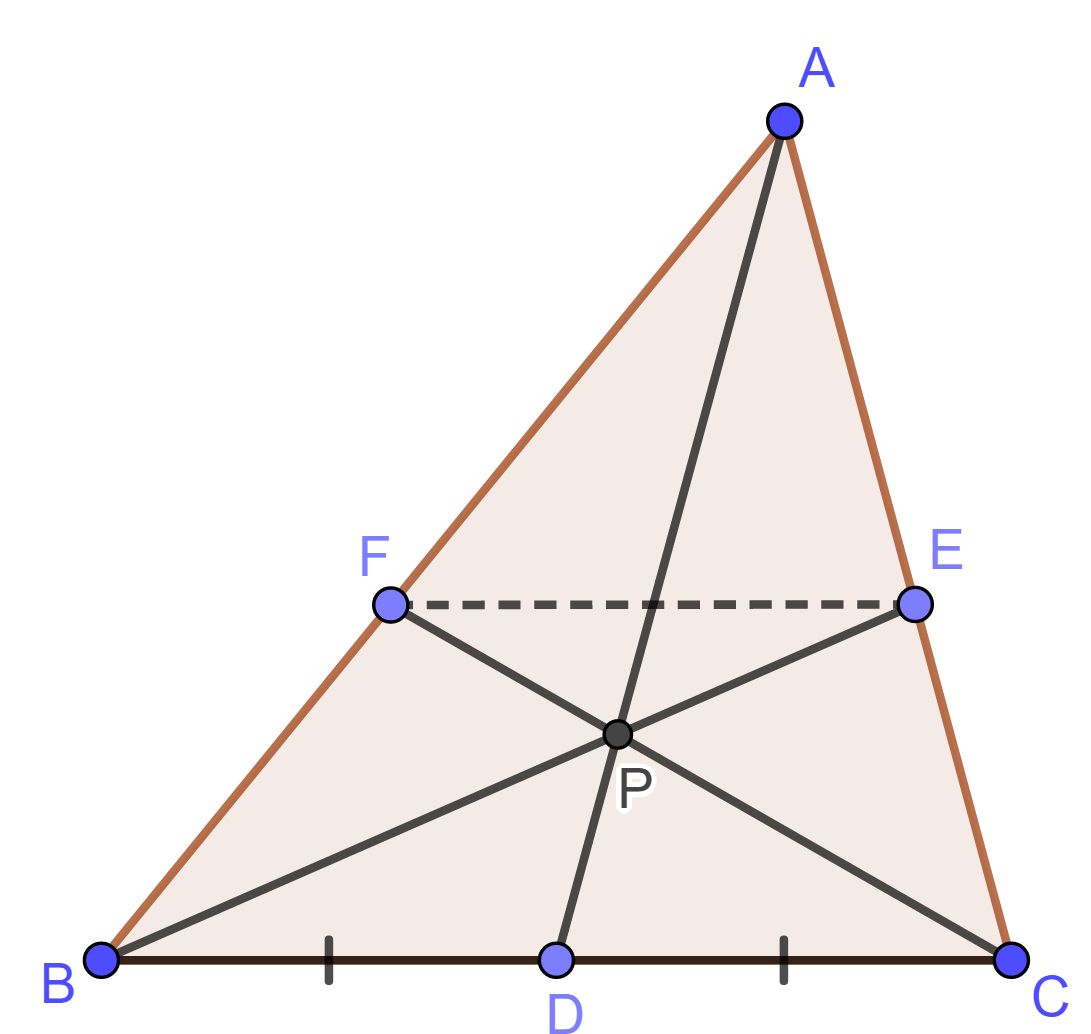
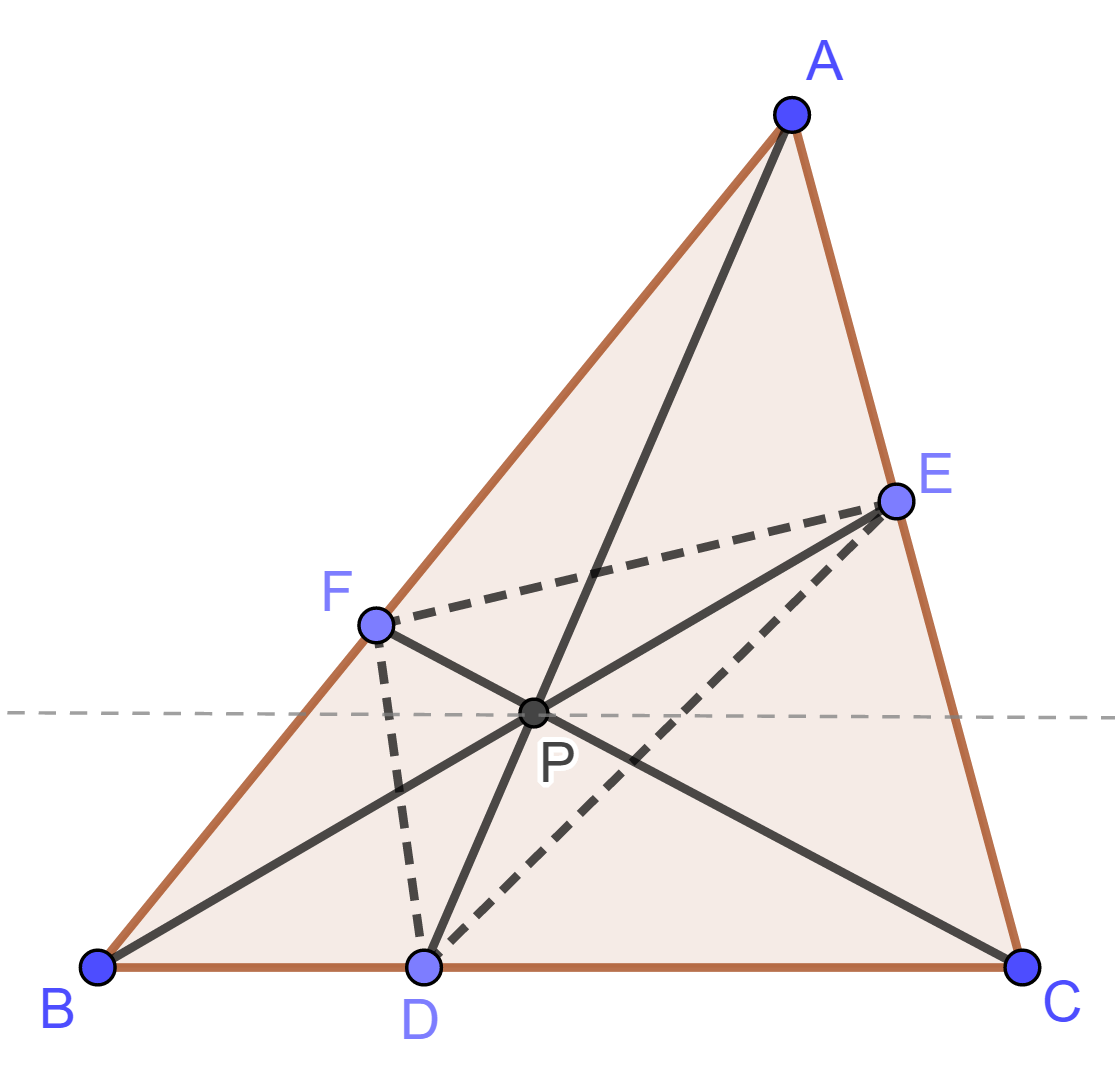
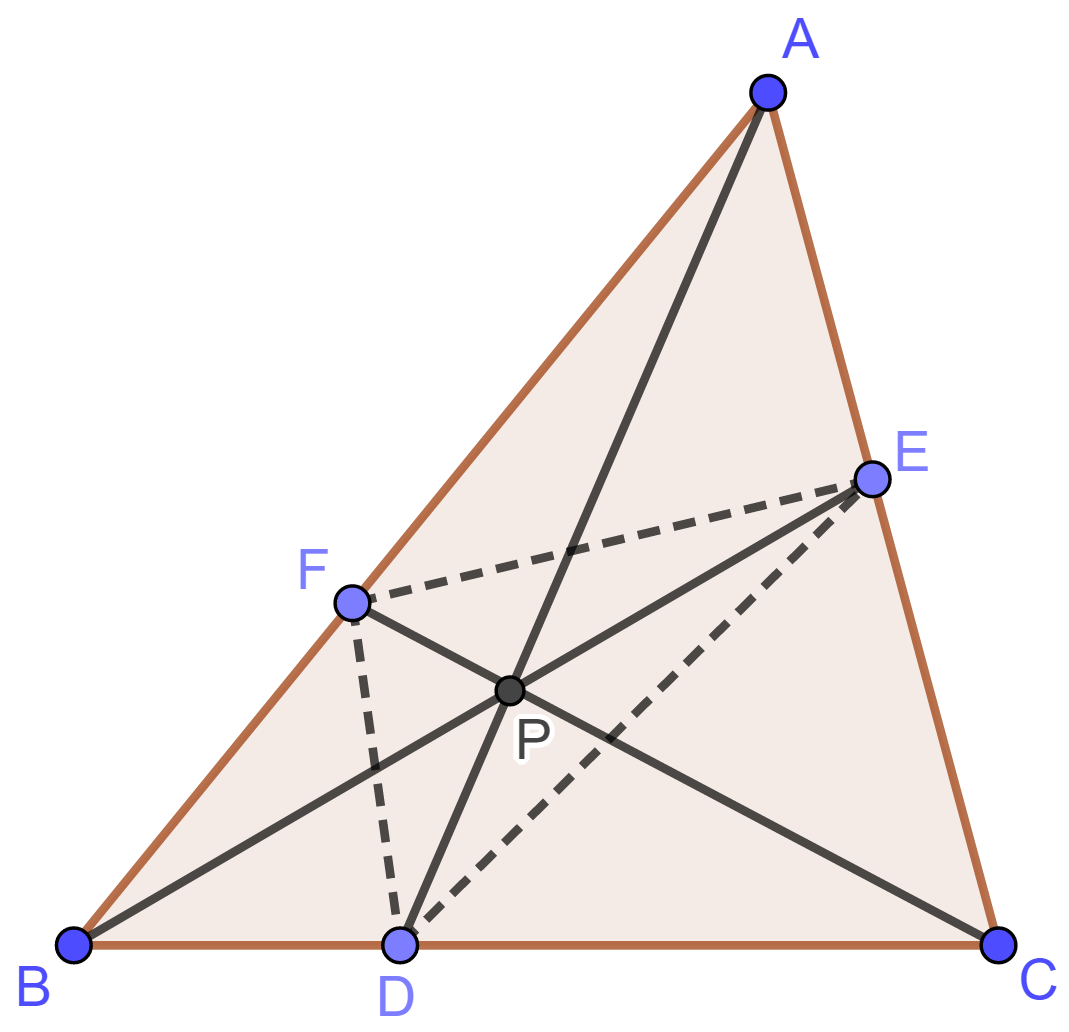
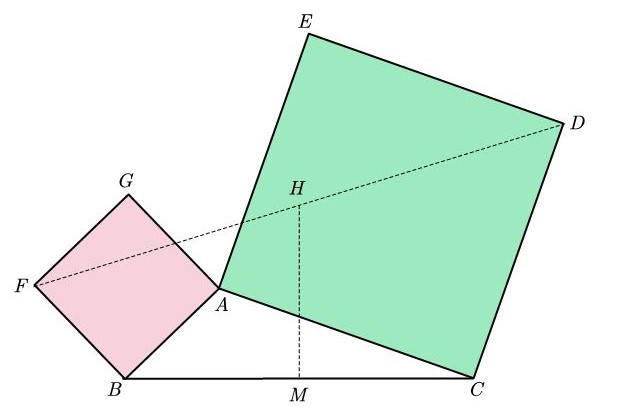
设梯形 $ABCD$ 有内接圆, 这里 $AD\parallel BC$. 内接圆与 $AB$, $CD$ 分别相切于 $K$, $L$; 与上下底 $AD$, $BC$ 分别相切于 $M$, $N$. 连接 $AN$ 和 $BM$, 设相交于点 $Q$. 连接 $KQ$.
证明: (1) $KQ\parallel AD$.
(2) $AK\cdot KB=CL\cdot LD$.